Delayed Gratification
Verifiable Delay Function in Lurk #
The MinRoot VDF came up in recent conversation, and it occurred to me that the easiest way to explain it would be just to write it down in Lurk. I wrote more about Lurk’s relationship to the VDF project in a recent blog post.
Since the result was quite simple and demonstrates some interesting things relating to Lurk, finite fields, and VDFs generally, I decided to present it here – along with some light commentary. Depending on your knowledge, some of what follows may be quite obvious or somewhat puzzling. My hope is that any puzzling parts nevertheless stimulate further thought. Puzzles are good, and sometimes they take time to solve. This post isn’t meant to be a tutorial or deep explanation. It’s just a quick tour of how Lurk can be applied to a real-world problem.
A verifiable delay function based on computation performs irreducible sequential computation, requiring the passage of time – but can still be verified quickly. Like the general Nova VDF project, our example here will use a (Nova) SNARK for the proof. This means proof verification will take a constant time regardless of how long we iterate the delay function. Proof generation, however, is linear in the work required to actually perform the verification computation. In theory, using succinct IVC such as Nova would allow us to make an incremental proof of the delay function directly. However, this would be needlessly expensive and difficult. To make producing our SNARK cheaper, we choose a function whose inverse can be calculated much more cheaply. Then we use the inverse to check the result of evaluation in a SNARK.
Just for fun, and in order to highlight how the math and performance characteristics relate, we’ll implement this VDF in Lurk now. The code used for this demo is available here. I ran it from the clutch directory at the root of the lurk-rs repo.
➜ clutch git:(vdf-demo) ✗ bin/clutch --demo demo/vdf.lurk
Finished release [optimized] target(s) in 0.14s
Running `/Users/clwk/fil/lurk-rs/target/release/clutch --demo demo/vdf.lurk`
Lurk Clutch welcomes you.
The clutch --demo feature steps through expressions in a provided file, evaluating each in the clutch REPL.
!> ;; Hat tip to JP Aumasson.
!(defrec fastexp (lambda (b e)
(if (= e 0) 1
(if (< (/ e 2) 0) ; is e odd?
(* b (fastexp (* b b) (/ (- e 1) 2)))
(fastexp (* b b) (/ e 2))))))
FASTEXP
While auditing Lurk, JP wrote some crypto library functions, including an early version of this fast exponentiation algorithm. Note that the (inlined) parity predicate exploits Lurk’s definition of field element ordering. Specifically, the ‘largest’ elements of the scalar field are designated as negative. When doubled, they overflow, and since arithmetic is mod a prime, the result is odd. Therefore, odd numbers divided by two yield negative numbers.
!> (fastexp 2 5)
[133 iterations] => 32
It gives the expected result (after 133 iterations).
!> ;; (4p - 3) / 5
!(def r 23158417847463239084714197001737581570690445185553317903743794198714690358477)
R
This somewhat magical number is the exponent to which we can raise any element of the scalar field of Pallas to calculate its fifth root.
As suggested in the comment, we want a value that, when multiplied by five, yields $1 \mod (p - 1)$. This is because exponentiation in a prime field ( $\mathbb{Z}_{p}$ ) respects $b^{n} = b^{n \mod \phi(p)}$, where $\phi$ is Euler’s totient. In a prime field of order $p$, $\phi(p) = p - 1$. Ergo, $b^{n} = b^{n \mod(p-1)}$
Put more directly, we define $r$ such that ${(b^{r})}^{5} = b^{5r} = b$. This requires that $5r\equiv1\mod(p-1)$. Of course $4p-3\equiv1\mod(p-1)$ because $4(p-1)+1\equiv1\mod(p-1)$.
!> !(def fifth-root (lambda (n) (fastexp n r)))
FIFTH-ROOT
!> !(def fifth (lambda (n) (fastexp n 5)))
FIFTH
Now we can define a pair of complementary functions, one of which involves exponentiation to a large power (with many multiplications) and one of which exponentiates to a small power (requiring only three multiplications).
!> (fifth-root 42)
[9661 iterations] => 0x2e6606ca7e8983f71964677e06cd8fd13ee0d46bf3c3e52d3af1b80df06f730b
!> (fifth 0x2e6606ca7e8983f71964677e06cd8fd13ee0d46bf3c3e52d3af1b80df06f730b)
[140 iterations] => 42
As expected, these operations invert one another. Notice that fifth takes 69 times fewer iterations than fifth-root. ($9661 / 140 \approx 69$)
MinRoot defines a relatively simple round function that iteratively transforms its state using the expensive step function.
!> !(def round (lambda (state)
(let ((x (car state))
(y (car (cdr state)))
(i (car (cdr (cdr state)))))
(cons (fifth-root (+ x y))
(cons (+ x i)
(cons (+ i 1) nil))))))
ROUND
See the diagram below, which represents an instance of MinRoot using the cube root as step function.
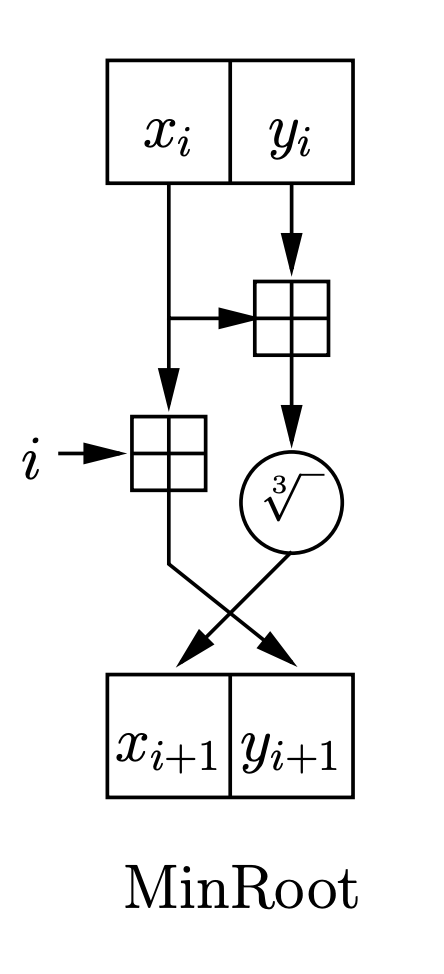
The (cheap) inverse uses the step function’s cheap inverse.
!> !(def inverse-round (lambda (state)
(let ((x (car state))
(y (car (cdr state)))
(i (car (cdr (cdr state))))
(new-i (- i 1))
(new-x (- y new-i))
(new-y (- (fifth x) new-x)))
(cons new-x (cons new-y (cons new-i nil))))))
INVERSE-ROUND
MinRoot itself iterates the round function for some specified number of rounds.
!> !(defrec minroot (lambda (state rounds)
(if (= rounds 0)
state
(minroot (round state) (- rounds 1)))))
MINROOT
!> !(defrec minroot-inverse (lambda (state rounds)
(if (= rounds 0)
state
(minroot-inverse (inverse-round state) (- rounds 1)))))
MINROOT-INVERSE
And we also implement its inverse.
!> (minroot '(123 456 1) 10)
[97438 iterations] => (0x27ec1d892ff1b85d98dd8e61509c0ce63b6954da8a743ee54b1f405cde722eb1 0x0da555f3ff604e853948466204d773c4c34d8cf38cea55351c9c97593613fb3b 11)
!> (minroot-inverse '(0x27ec1d892ff1b85d98dd8e61509c0ce63b6954da8a743ee54b1f405cde722eb1 0x0da555f3ff604e853948466204d773c4c34d8cf38cea55351c9c97593613fb3b 11) 10)
[2386 iterations] => (123 456 1)
Here we see that our implementation of inverse MinRoot can be used to recover the orignal state. Also, we see that the slow/forward direction takes only 40.8 times the number of iterations the slow/backward direction does, as opposed to 69x for the simple step function. The overhead of the wrapping decreases the asymmetry. Lurk is not a great language to use for a real VDF implementation!
!> !(prove)
Claim::PtrEvaluation elided.
"bafkr4ihoaqtkt3fa2gbcurqd6io4iqf4s7e63efknh7xxa65g4e4nkwdl4"
Nevertheless, we can make a succinct proof, and that proof will be very fast to verify, however many rounds the proof covers – so maybe Lurk is not so bad.
!> !(verify "bafkr4ihoaqtkt3fa2gbcurqd6io4iqf4s7e63efknh7xxa65g4e4nkwdl4")
T
Yep, it verifies. And yep, that’s fast.
Just for fun, I include a toy example application of a computational VDF like this one. We can use it for timelock encryption.
!> !(def timelock-encrypt (lambda (secret-key plaintext rounds)
(let ((ciphertext (+ secret-key plaintext))
(timelocked-key-state (minroot-inverse (cons secret-key '(0 1)) rounds)))
(cons timelocked-key-state ciphertext))))
TIMELOCK-ENCRYPT
We define timelock-encrypt to take a secret key, some plaintext (just a field element in this example), and a number of rounds. We encrypt the plaintext by adding the random key, then we timelock the key with minroot-inverse. Because minroot-inverse is relatively fast, we can obtain a timelocked decryption key quickly.
!> !(def timelock-decrypt (lambda (timelocked-key-state ciphertext rounds)
(let ((secret-key (car (minroot timelocked-key-state rounds)))
(plaintext (- ciphertext secret-key)))
plaintext)))
TIMELOCK-DECRYPT
To decrypt, we’ll reverse the process. First we recover the secret key by applying MinRoot. This will be ~41 times slower than our encryption process. Then we use the recovered secret key to decrypt the ciphertext.
!> ; !> (timelock-encrypt (num (commit <REDACTED SECRET KEY>)) <REDACTED PLAINTEXT> 10000)
!> ;; [2370068 iterations] => ((0x2b7a3b8ddd37f5729671b40f14ea588eb74e0474516503cae76114c80c3e68b3 0x39766ed0c1d5a61b0a0b5146585f01ea78bac01860ce0f8653bb098d42efcce3 0x40000000000000000000000000000000224698fc0994a8dd8c46eb20ffffd8f2) . 0x0fbc16c244caeec63f5e0316c9b36ad5eba0b1c10f7ecf5d681a911e9dfa74d0)
I’ve redacted the secrets, but this is the result of my private execution of timelock-encrypt.
!> (timelock-decrypt ;; timelocked key state
'(0x2b7a3b8ddd37f5729671b40f14ea588eb74e0474516503cae76114c80c3e68b3
0x39766ed0c1d5a61b0a0b5146585f01ea78bac01860ce0f8653bb098d42efcce3
0x40000000000000000000000000000000224698fc0994a8dd8c46eb20ffffd8f2)
;; ciphertext
0x0fbc16c244caeec63f5e0316c9b36ad5eba0b1c10f7ecf5d681a911e9dfa74d0
;; rounds
10000)
;; [97420050 iterations] => <REDACTED PLAINTEXT>
I also ran timelock-decrypt as above, to make sure it would complete. It did and took 5-6 minutes on my laptop. My original correspondent, Matej, said it took about eight minutes on his machine.
Of course, if we want to use VDFs to ensure the passage of time, variability in execution time is problematic. We would like our estimates of minimum running time to provide as tight a bound as possible. In order to accomplish this, we can build custom hardware (ASICs) designed to evaluate MinRoot as fast as possible. Here are some pretty pictures of the prototype Supranational has built. The ASIC evaluator can perform 3.7M MinRoot rounds per second. So our measly 10,000 rounds would only take 200 µs.
If you’re feeling adventurous, want to try Lurk, and to viscerally experience this toy puzzle, try running the demo yourself, including the timelock decryption. If you’re lazy and don’t have time, get your hands on on one of these babies:


Although Lurk Alpha involves some unavoidable overhead, it’s also far from optimized. One motivation in posting these timings is in the spirit of optimization, to encourage the Lurk Lab team to eventually eliminate incidental inefficiency from our evaluation. In addition to simple optimization efforts, it’s important to note that once Nova supports SuperNova, Lurk will be able to support ‘real’ VDF proofs. Likewise, nothing will stop a Lurk application from making use of a hardware VDF if needed.
The important point is that Lurk is deeply compatible with these cryptographic primitives. It can be used to explore, reason about, and script interesting algorithms quickly, and to interact with the results. As an example, although timelock encryption is a known application of a MinRoot-like VDF, we didn’t give this application much thought while working through the development of the evaluator ASIC. When I mentioned the example given above to Kelly at Supranational, he noted that the current ASIC prototype didn’t provide on-chip support for the fast direction. That means that using the technology available in the world today, a timelock encryption application like above would need to use CPU for the ‘fast encryption’ phase. This would reduce what should be an 85x speedup (on ASIC) to ~8.5x on CPU. However, as a direct consequence of applied playfulness and the power of the lightweight, interactive experimentation Lurk facilitates, we noticed this then. The final evaluator ASIC could have included support for the fast direction too, and somewhat powerful (85x asymmetry) timelock encryption would be made possible.
