Lurk Circuit Specification
$\global\def\var#1{\footnotesize{\textsf{#1}}}$ $\global\def\gad#1{\footnotesize{\textsf{#1}}}$ $\global\def\fun#1{\footnotesize{\textsf{#1}}}$ $\global\def\cir#1{\footnotesize{\text{#1}}}$ $\global\def\cirtitle#1{\footnotesize{\bold{#1}}~}$ $\global\def\cirio#1{\footnotesize{\bold{#1}}~}$ $\global\def\com#1{\footnotesize{\text{#1}}~}$
$\bf{Disclaimer}$: This spec is a work in progress. It is an ongoing project and will continue to be refined over time. Questions about the circuit can be posed in the Lurk Zulip server.
Introduction #
Zero-Knowledge Proofs 1 are cryptographic primitives that allow some entity (the prover) to prove to another party (the verifier) the validity of some statement or relation. Today there are many efficient constructions of NIZK proof systems, with different trade-offs, as well as several implementations of the proving systems.
Every proving system, as described in the zk-Interface 2, can be divided into the backend, which is the portion of the software that contains the implementation of the underlying cryptographic protocol, and the frontend, which provides means to express statements in a convenient language, allowing to prove such statements in zero knowledge by compiling them into a low-level representation.
The backend of a proving system consists of the key generation, proving and verification algorithms. It proves statements where the instance and witness are expressed as variable assignments, and relations are expressed via low-level languages. The most common instance of such a low-level language is R1CS, a generalization of arithmetic circuits, introduced in 3 and used in many other proof systems (see 4, 5, 6, 7 among others).
Lurk is a proving frontend which accepts high-level statements written in the form of a Lisp dialect, and produces a low-level proof representation thereof specifically tailored to work well with a certain class of proving backends. Indeed, Lurk produces proof statements shaped as chained but distinct iterations of a single abstract state machine8 represented in R1CS. As the components of the low-level proof statement only differ in their assignment of inputs and outputs, Lurk’s outputs are particularly well suited to cryptographic backends that support recursion, or more generally proof aggregation. As an implementation, Lurk currently focuses on producing statements in R1CS, and supports two backends: Nova 9 and SnarkPack 10.
The Lurk frontend consists of the following:
- The specification of a high-level language for expressing statements.
- A compiler that converts relations expressed in the high-level language into the low-level relations suitable for some backends. This leverages a library of “gadgets” consisting of useful and hand-optimized building blocks for certain primitive statements.
- Instance reduction: conversion of the instance in a high-level statement to a low-level instance
- Witness reduction: conversion of the witness to a high-level statement to a lowlevel witness (e.g., assignment to witness variables).
Lurk decomposes relations expressed in its Lisp-like source language into iterations of an abstract state machine (ASM), which implements a deterministic interpreter for this language. The workings of the step function of this state machine is detailed in the reduction section below.
At a high level, Lurk’s ASM manages four constructs:
- a library of R1CS gadgets, which allow translating primitive blocks of the source language directly into arithmetic sub-circuits,
- a continuation stack, that allows deferring the evaluation of sub-parts of the current program, or upacking deferred part of the computation in the translation of the currently-selected portion of the AST is finished,
- a reduction strategy, that allows selecting sub-parts of the input AST for evaluation deterministically,
- a strict hashing discipline for Lurk programs, which allows the prover to memoize the translation of portions of the input program, while producing cryptographic hashes that bind the prover to a specific source program.
This step function proceeds repeatedly until the input program is fully evaluated.
Lurk #
Lurk is a functional programming language based on Scheme and Common Lisp. An important aspect of its design is Continuation Passing Style (CPS)11, where the control flow of programs can be managed through the use of continuations. Continuations are recursive data structures that can be used as part of a representation of generic computations. In particular, for each basic operation in a certain computation, a continuation is used as a pointer to the rest of the computation, i.e. it indicates what must happen after this basic operation is computed. Concretely, it takes the form of a stack of continuations that we will describe in greater detail later on. This technique allows us to divide a program into small parts and build a small circuit for each part. We will summarize the main concepts involved in the design of the language, which should enable the reader to understand how zero-knowledge proofs 7 9 12 are constructed in Lurk.
In this section, we provide a summary of Lurk’s main elements. An expression represents a computation involving literals, variables, operations and procedures. Variables are handled by an environment , which is responsible for binding variables to values. We also use continuations to indicate what must be done to finish the computation.
The system’s I/O is formed by an expression, an environment, and a continuation. Understanding these 3 elements is essential to comprehending Lurk. Each element is represented as a pointer, which is implemented using hash functions. In particular, we use Poseidon 14 to instantiate our pointers.
The environment has a list of bindings, which correspond to a mapping between variables and values at a certain point in time. The mapping of these local bindings is valid only for a specific evaluation of an expression. On the other hand, the global state is represented by the store, which behaves as a memory of the system. The store is global, while the environment is local.
Language overview #
- t, nil: are self-evaluating and represent
trueandfalse, respectively. - if: has the format
(<test> <consequent> <alternate>)and represents a conditional expression. It must receive all 3 parameters, where the<test>is an expression used to select the result; the<consequent>is selected if the<test>evaluat es to non-nil; and<alternate>is selected otherwise. Unlike other programming languages, the<alternate>expression is mandatory. - lambda: has the format
(lambda <formals> <body>)and represents a procedure. The environment when the lambda expression is evaluated is used as a closure, which is extended with<formals>, a list of variables. The unique expression in the<body>is evaluated and returned as the result of the lambda expression. - let: has the format
(let <bindings> <body>)and represents an assignment expression, where<bindings>represents a list of pairs in the form(<variable>, <init>); and<body>is a unique expression. - letrec: has the same format as
<let>expressions, following the same rules, but also allowing recursion. - quote: has the format
(quote <datum>)or(’ <datum>)and evaluates to<datum>. - atom: has the format
(atom <e>), and it evaluates totif<e>is not a list, and evaluates tonilotherwise. - cons, strcons car, cdr: The expression
(cons <a> <d>)produces a pair whosecaris<a>andcdris<d>. When<a>evaluates to a character and<d>evaluates to a string, we have thatstrcons <a> <d>produces to a string. In this situation we have thatcar <e>returns the first character when<e>is a string. Correspondingly,cdr <e>returns a string obtained from removing the first character from<e>. - arithmetic operations: has the format
(<op> <e1> <e2>), where<op>corresponds to an arithmetic operation(+, -, *, /).<e1>is evaluated before<e2>and the operation is carried out in the finite field that is used in the subjacent zero-knowledge backend. - equality: has the format
(<op> <e1> <e2>), where<op>can be either=oreq. The equality symbol=is used to compare expressions whose result is a number (finite field elements), while the symboleqis used to compare pointers. - emit: has the format
(emit <e>)and is used to return the result of the evaluation of<e>as a public value, which can be used to define the instance of the zero-knowledge statement. - begin: has the format
(begin <e> ...). The sequence of expressions is evaluated from left to right and the last result is returned. - current env: returns the current environment represented as an association list.
- eval: has the format
(eval <exp>)or(eval <exp> <env>). The evaluation of<exp>is used as an expression in the environment obtained from the evaluation of<env>. If no<env>is provided, an empty environment is used. - hide: has the format
(hide <exp> <secret>). Return the commitment of<exp>using secret<secret>. - commit: has the the format
(commit <exp>). Compute the commitment of<exp>. - secret: has the format
(secret <comm>). Return the secret used to generate the commitment<comm>, if known. - open: has the format
(open <comm>). Return the value used to generate the commitment<comm>, if known. - comm: has the format
(comm <data>). Change the tag of<data>tocomm. - num: has the format
(num <data>). Change the tag of<data>tonum. - char: has the format
(char <data>). Change the tag of<data>to<char>. - u64: has the format
(u64 <num>). Coerce<num>to be a 64-bit unsigned integer.
Fibonacci example #
Here is an example code snippet that implements the Fibonacci sequence. You can click the $\small\blacktriangleright$ button to display the output.
output goes here$$ \rm{\small{Figure~1: Fibonacci~example}} $$
Circuit overview #
In this section, we give a short description of Lurk’s circuit. Important concepts are introduced to help the reader better understand the purpose of certain components and how they interface with each other.
High-level description #
A Lurk program consists of a sequence of reduction steps, or iterations, which are mapped to frames. A set of frames is grouped into a MultiFrame object. Each frame is represented by a CircuitFrame and a Circuit is a sequence of CircuitFrames where the output of one frame is connected to the input of the next, mimicking the evaluation of Lurk expressions. For instance, in the Fibonacci example above, we have 521 iterations, each one mapped into a frame.
In eval.rs, the function reduce_with_witness() computes reduction steps with their witnesses. We provide an implementation of this computation in the circuit using the functions $\cir{Reduce-expression}()$ and $\cir{Apply-Continuation}()$ in the file circuit_frame.rs. Global symbols are pre-computed Lurk symbols that can be easily compared with symbols found during expression evaluation.
To reduce an expression, we distinguish between two cases: atoms, such as symbols, and lists, which are more complicated expressions composed of an operation in the first position and other elements that can be atoms or nested lists. In $\cir{Reduce-Sym}()$, we reduce symbols using comparisons among symbols that require allocation of variables and pointers in the circuit, Boolean logic, and conditionals. For example, $\cir{Reduce-Sym}()$ is used to find the value of a variable. We update the environment and the store accordingly.
The cons function is a crucial building block in functional languages like Lurk. It concatenates car and cdr, allowing us to break down expressions into smaller pieces. In $\cir{Reduce-Cons}()$, we handle each possible Lurk expression that is constructed using cons. We allocate auxiliary variables in the circuit for later use and use a $\gad{CAR-CDR-NAMED}()$ gadget as a building block. We include a clause in a multicase gadget for each situation depending on the type of expression we are handling, and select the desired result based on the head of the expression using car. Finally, we return the result of the multicase.
Another important function is $\cir{Apply-Continuation}()$. In order to finish a reduction step, we must calculate the output of the frame. Each iteration has a continuation tag that requires a computation of the next expression, environment, continuation, and thunk. Therefore, we have to constrain the system to prove we are computing the correct elements, and we have to allocate pointers to use them later. This task is executed in 2 stages:
- Some continuations require the calculation of new pointers, while others don’t. For those that need new pointers, since the implementation of pointers requires a hash computation and because hashes are expensive in the circuit, we use a multicase to select the appropriate hash preimage. Then we can compute the hashes just once. This allows us to avoid computing unnecessary hashes.
- We then use another multicase to select the continuation results.
Gadgets #
To construct the circuit, we use gadgets and auxiliary functions as building blocks. These gadgets are fragments of emitted code generated by the Lurk compiler, which represent the translation of primitive operations of the Lurk language into the low-level language accepted by cryptographic proof backends. Each gadget incorporates constraints that convey the semantics of the source language in the low-level language of arithmetic circuits. For instance, when we interpret an expression like $a + b$, the emitted gadget not only computes the addition but also takes into account the max values of $a$ and $b$ when interpreted as u64, along with the overflow semantics of their sum - even when the gadget manipulates primitive addition operations on 256-bit numbers.
Gadgets are denoted in all caps, and composition of gadgets is shown using a dark gray color. Full details of the gadgets, such as the number of constraints of each component and their implementation description, will be provided in the Low-level description section.
- Variable types: In the circuit we allow variable to have the following types:
- AllocatedNum: represents a field element in the circuit.
- AllocatedPtr: represents a pointer in the circuit, which is given by 2 AllocatedNums, denoted by $\var{tag}()$ and $\var{hash}()$ respectively.
- AllocatedContPtr: represents a continuation pointer in the circuit. Silimilarly to AllocatedPtr, it is formed by 2 AllocatedNums.
- Boolean: represents a bool in the circuit. It can be used both for allocated values or as constants. In the case it represents an allocated value, this value is enforced to be 0 or 1.
Some gadgets, such as $\gad{NOT}$, refer to other circuits - in this case the Boolean variable being negated. This reflects that arithmetic circuits have input and output variables, and can therefore be connected to each other. In this case, the circuit for $\gad{NOT}$ will have its input wired to the output of the circuit generating the Boolean variable passed as its argument.
Syntax :
Let: creates a variable in the circuit.
Call: allocate a gadget inside a circuit, used when gadgets have no return values.
Return: defines the output of a circuit.
We use dot notation to access global variables:
- Let $\var{symbol-tag} = \var{globals.sym-tag}$.
We use dot notation to access gadget’s helper methods:
- Let $m = \gad{CASE-CLAUSES}()$.
- Call $m.\gad{ADD-CLAUSE}(k, c)$.
Tuples and vectors: syntactic sugar to manipulate circuit variables.
Boolean operations: used to handle bit operations like conjunctions, disjunctions, negations, and bit decomposition.
- Let $o = \gad{AND}(i_1, i_2, \dots)$: Receives a variadic number of input variables of type Boolean and returns another Boolean representing the conjunction of the input variables.
- Let $o = \gad{OR}(i_1, i_2, \dots)$: Receives a variadic number of input variables of type Boolean and returns another Boolean representing the disjunction of the input variables.
- Let $\var{negated-b} = b.\gad{NOT}()$: Every variable $b$ of type Boolean has an auxiliary method called NOT, which receives no input and returns another Boolean representing the negation of $b$.
Equality: allows equality tests of allocated variables.
- Let $\var{is-equal} = \gad{ALLOC-EQUAL}(a, b)$: The Boolean variable $\var{is-equal}$ is true if and only if $a$ is equal to $b$.
- $\gad{EQUAL}(a, b)$: enforces $a$ equal to $b$.
- Let $\var{is-zero} = \gad{ALLOC-IS-ZERO}(a)$: The Boolean variable $\var{is-zero}$ is true if and only if $a$ is zero.
Pick: used for ternary operators.
- Let $a = \gad{PICK}(\var{cond}, a, b)$: If $\var{cond}$ is true, return $a$, otherwise return $b$.
Implication: used for constraints in the form: if $\small{a}$ is true, then $\small{b}$ is true, where $\small{a}$ and $\small{b}$ are expressions that evaluate to Boolean values.
- Call $\gad{IMPLIES-EQUAL}(\var{cond}, a, b)$: If $\var{cond}$ is true, then $a$ is enforced to be equal to $b$.
Arithmetic operations: used to constrain arithmetic operations $\rm{\footnotesize{(+,~-,~*,~/)}}$ in the subjacent finite field.
- Let $c = \gad{SUM}(a, b)$: $c$ is enforced to be $a + b$.
- Let $c = \gad{SUB}(a, b)$: $c$ is enforced to be $a - b$.
- Let $c = \gad{MUL}(a, b)$: $c$ is enforced to be $a . b$.
- Let $c = \gad{DIV}(a, b)$: $c$ is enforced to be $a . b^{-1}$.
Pointers: formed by a tag, which allows us to identify the type of the pointer, and a hash that links the pointer to its content, which is given by the hash preimage.
- Let $a = \gad{ALLOC-PTR}(\var{pointer})$: Allocates a pointer in the circuit.
Data: functions can allocate different types of data by using pointers. Later, data can be accessed non-deterministically by providing the witness that corresponds to the hash preimage.
- Let $\var{hash} = \gad{CONSTRUCT-CONS}(\var{car}, \var{cdr})$: Computes a hash function over $\var{car}$ and $\var{cdr}$.
- Let $\var{hash} = \gad{CONSTRUCT-FUN}(\var{args}, \var{body}, \var{env})$: Computes a hash function over $\var{args}$, $\var{body}$ and $\var{env}$.
- Let $\var{hash} = \gad{CONSTRUCT-LIST}(\var{args}[])$: Computes a hash function over args by using a sequence of cons.
- Let $\var{hash} = \gad{CONSTRUCT}(\var{comp1}, \var{comp2}, \var{comp3}, \var{comp4})$: computes a hash function over $\var{comp1}, \var{comp2}, \var{comp3}, \var{comp4}$.
Multicase: used to select results based on certain selection tags. It is basically a set of cases that share the same set of selection tags. A multicase whose size is equal to 1 is the same as a regular case.
- Let $\var{case-clauses} = \gad{CASE-CLAUSES}()$: a list of clauses for a $\gad{CASE}$ gadget.
- Let $\var{result} = \gad{CASE}(\var{key}, \var{clauses}, \var{default})$: the result of using key to select a value from clauses. If no clause is found, return default.
- Let $\var{multicase-clauses} = \gad{MULTICASE-CLAUSES}()$: A list of clauses for a $\gad{MULTICASE}$ gadget.
- Let $\var{result} = \gad{MULTICASE}(\var{key}, \var{clauses}, \var{default})$: the result of using key to select a value from clauses. If no clause is found, return default.
Auxiliary circuits: #
- Comparisons: computes the comparison of allocated variables.
- Enforce n bits: Enforce a certain allocated number can be represented using $n$ bits.
Circuit specification #
This section describes the Lurk circuit in detail. We present the high-level algorithms first to help readers understand our architectural decisions, become familiar with the notation, and comprehend how components are interconnected. We then provide the low-level algorithms, which explain how we construct R1CS constraints for each building block in this document.
Backends #
Currently, we support two backends: Groth16 7 and Nova 9. Both are based on R1CS constraints, enabling us to create a single circuit that works with both backends. However, there is an essential difference between the two. Groth16 requires a trusted setup for each circuit, which we want to avoid since updating the circuit would require another ceremony for the new trusted setup. Conversely, Nova doesn’t need a trusted setup. Moreover, Nova allows recursive composition of proofs, making it a practical and exciting alternative. In particular, it fits well into the Lurk circuit since we can fold Lurk frames using Nova’s folding technique. Regrettably, recursive composition is beyond the scope of this document.
From the application layer perspective, the only difference between these systems is the underlying finite field. Specifically, it means that programs like $\rm{\footnotesize{(- 1 ~0)}}$ evaluate to different numbers in each case.
Next we summarize the main characteristics of each system:
- Groth16 7 is implemented over the BLS12-381 elliptic curve. The subjacent Finite Field for Lurk applications is defined over the following prime: 0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001
- Nova 9 is based on the cycle of elliptic curves named Pallas and Vesta 15. The underlying Finite Field is defined over the following prime: 0x40000000000000000000000000000000224698fc0994a8dd8c46eb2100000001
Lurk data are constructed using finite field elements. In subsequent sections we show how other data types are represented using these elements.
We denote the finite field by F in order to provide an homogeneous description of Lurk circuits, but it is important to note that, depending on the chosen backend, a different prime is used, which may lead to distinct behavior in some situations (as, for example, when modular reductions are involved).
Main concepts #
Here we describe how Lurk evaluation works. Later we will show how the circuit implements the same components.
A Lurk expression is evaluated step-by-step by applying a reduction method. The next step to be applied is called a continuation. In this next example we see how a simple program is evaluated.
> (atom 42)
INFO lurk::eval > Frame: 0 Expr: (ATOM 42)
Env: NIL
Cont: Outermost
INFO lurk::eval > Frame: 1 Expr: 42
Env: NIL
Cont: Unop{ operator: Atom, continuation: Outermost }
INFO lurk::eval > Frame: 2 Expr: T
Env: NIL
Cont: Terminal
[2 iterations] => T
$$ \rm{\small{Figure~2: Atom~example}} $$
The evaluation process begins by identifying the atom operation. Once the operation is detected, we can create a corresponding continuation, called unop, which is short for unary operation. In the second step, we evaluate the unique operand, the number 42, which results in itself. Next, we apply the atom operation to 42 and obtain the symbol T.
The continuation for the atom operation requires only one expression as input, which in this case is the number 42. We then need to find a way to return this to the caller, which is Frame 0. After this step, we can return the result of evaluating atom over 42, which is T, and terminate the computation since it is the outermost continuation.
The unary operator follows a specific structure, consisting of the operator and the continuation, which is represented as Lurk data by finite field elements. The continuation is represented by a tag and a pointer. To look up the pointer content, we use dictionaries, which are hash maps used to store data in a content-addressable way. A hash function is calculated over the content to generate an index, which is used to address the data efficiently. It is important to note that we do not use dictionaries in the circuit. Instead, we provide the witness that corresponds to the hash preimage and the result non-deterministically. Therefore, we do not need to look up any table to find the result since the result is already there.
Pointers #
A pointer consists of two field elements: a tag and a raw pointer. The tag serves the purpose of distinguishing between different types of pointers, which is important because each tag corresponds to a distinct data structure behind the pointer. The content of the pointer has a structure that varies according to its type, and this type can be determined by the tag. The raw pointer is a dictionary index that can be used to efficiently access the content. Pointers are versatile and can be used to store Lurk expressions, allowing for the expression of recursive expressions. Additionally, pointers can be used to represent the environment, as described in the Environment Section.
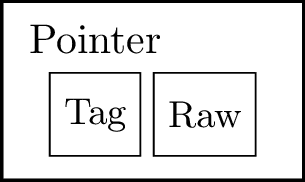
Figure 3: Pointer
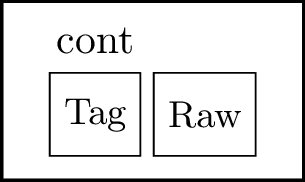
Figure 4: Continuation pointer
A continuation pointer, denoted by $\rm{\footnotesize{cont}}$, is also defined as 2 field elements: a continuation tag and a raw pointer. It works in the same way as regular pointers, but it is restricted to continuations. While this differentiation is not necessary, it enhances the design organization by separating components based on their functionality. If we want continuations to be first class, we would have to treat them like regular pointers.
A raw pointer is a 32-bit integer (encoded naturally as a field element) that represents an index in some of the dictionaries managed by the store. This enables efficient recovery of the pointer’s content. If the raw pointer is negative, it encodes an opaque pointer, which implies that the store is not aware of it.
Expressions #
Expressions are recursive data structures containing nested operations involving literal values, variables, and operations. It can represent arithmetic expressions like $\rm{\footnotesize{(+~10~32)}}$, or lambda expressions such as $\rm{\footnotesize{(lambda~(x)~x)}}$. An anonymous function that returns the received input argument. Here is a list of Lurk expressions:
- nil. The
nilsymbol is a self-evaluating expression. Since it is used frequently, we have a global pointer to represent it. - cons(pointer, pointer). A
consexpression receives two input arguments, which are given by generic pointers. Both expressions are concatenated, forming a new list, which is inserted into the store. - comm(F, pointer). A comm operation receives as input a secret value, represented as a field element, and a second expression, which represents the content of the commitment. The output is a pointer to a field element, which is the commitment using Poseidon hash.
- sym(string). A Lurk symbol is given by a string, which may be either a restricted Lurk symbol like
cons,car,cdr,if, orlet, or a new symbol, defined usingletorletrec. It could also be a local symbol, as, for example, in arguments of lambda expressions. - fun(pointer, pointer, pointer). Each pointer represents the arguments, the body, and the closed environment, respectively.
- num(F). A
numexpression is represented by a field element, and the output is a pointer to it. - str(string). A string expression is represented as a list of
char, recursively interpreted as acons(char, string), where the first element is somechar, and the rest of the string is another string. - thunk(pointer, cont). A
thunkexpression contains a pointer to an expression that must be evaluated before calling the continuation, which is the second argument. It is an important building block for constructing special continuations like tail, outermost, terminal, and error continuations. - opaque(pointer). LurkIt allows for opaque pointers, where the content of the pointer is not known by the store. Such pointers can’t be resolved, and they are useful for manipulation of private data (for example).
- char(char). A
charexpression is represented by achartype, which is encoded as a field element naturally.
Figure 5 shows the tree structure of Lurk expressions.
Figure 5: Lurk expression example
Continuations #
Continuations are data structures containing all the information necessary to continue some computation. Different continuations require different information. Two important continuations are unop and binop, which respectively denote the continuation for unary and binary operations. In order to evaluate the second argument of a binop we require a binop2 continuation.
- outermost. It is the continuation that points to the initial frame.
- call0(cont). It is represented by a continuation pointer that contains the function to be called.
- call(pointer, pointer, cont), where the first argument corresponds to the unevaled argument, the second is the saved environment, and the third is the continuation. It creates a $ \rm{\footnotesize{call_2}} $ continuation that will be able to evaluate the argument and finish the call procedure.
- call2(pointer, pointer, cont), where the first argument corresponds to the function to be called, the second is the saved environment, and the third is the continuation. It creates a tail continuation, which will evaluate the body of the function.
- tail(pointer, cont). A tail continuation allows nested tails that may be constructed after evaluation of recursive operations to be compressed down to a single step that returns the expected continuation, returning a thunk.
- cont-error. This represents the continuation after some error happened. It is equivalent to a terminal continuation, because if Lurk finds an error, then a cont-error is returned as the output of the Lurk program evaluation.
- lookup(pointer, cont). This continuation is responsible for doing lookups in the environment, returning a thunk.
- unop(operator, cont). The unary operator continuation doesn’t have an unevaluated argument, therefore it can be executed in a single step, returning a thunk.
- binop(operator, pointer, pointer, cont). This is the first step of a binary operator, where the unevaluated argument pointer is used to construct a $ \rm{\footnotesize{binop2}} $ continuation.
- binop2(operator, pointer, cont). The second step of the binary operator can finish the work returning a thunk.
- if(pointer, cont). This continuation is used to select which unevaluated expression will be returned to be evaluated next, according to the conditional expression that is currently being evaluated.
- let(pointer, pointer, pointer, cont). The first argument represents a variable, the second is the body, the third is the saved environment, while the fourth is the continuation. We have that the continuation of a let expression is to extend the environment with the variable and return the body.
- letrec(pointer, pointer, pointer, cont). Similarly to let, but allowing recursion.
- dummy. A dummy continuation is useful for maintaining some invariants in the design, allowing us to control the call of the apply-continuation algorithm.
- terminal. It is the final continuation of a successful Lurk program evaluation.
- emit(pointer). This continuation is useful for creating intermediary publicly visible output of Lurk evaluations.
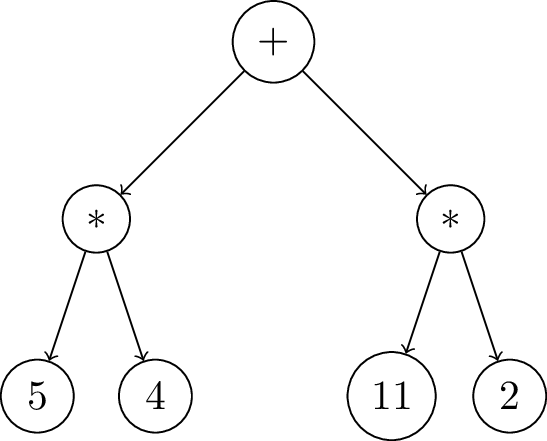
In the below Figures, we show the DAG structure of Lurk continuations. For each specific point in time, this DAG is just a stack of continuations, starting with the outermost continuation (see left part of Figure 6), growing and reducing the stack accordingly as we reduce expressions. As an example, we evaluate $\rm{\footnotesize{\lparen+~\lparen*~4~5\rparen~\lparen*~11~2\rparen\rparen}}$.
Expression DAG

Continuation DAG
$$ \rm{\small{Figure~6: Reduction~step~1}} $$
Expression DAG
Continuation DAG
$$ \rm{\small{Figure~7: Reduction~step~2}} $$
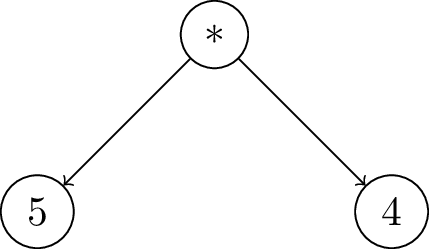
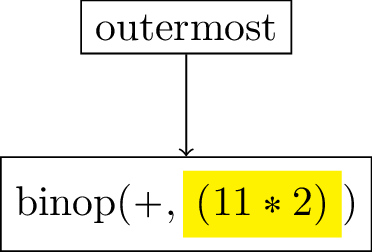
After we compute one reduction step over the input expression, we find a + operator at the head of the expression, which is one among many possible binary operations supported by Lurk. In order to evaluate the two input arguments of this binary operation, we need to create two continuations, respectively binop and binop2, saving context data to allow the calculation and saving the previous continuation to be able to return the control flow to the expected place.
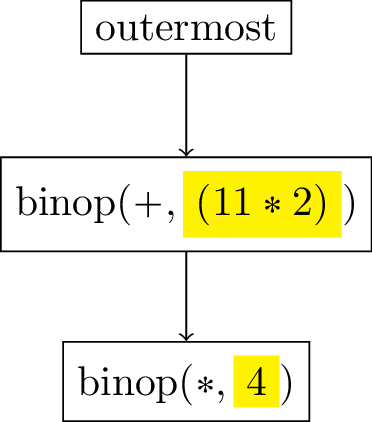
The first step is to create a binop continuation, as shown in Figure 7, saving the second argument, which is not yet evaluated, such that we evaluate it in the next reduction step.
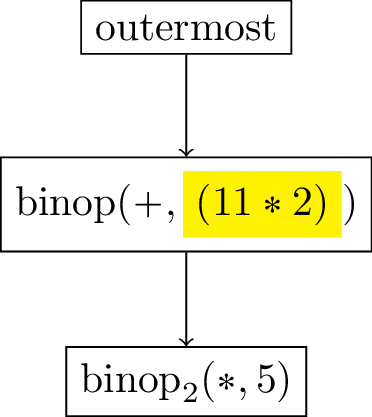
Because the first argument itself is the binary operation $\rm{\footnotesize{\lparen*~4~5\rparen}}$ (see Figure 7), we need to repeat the same logic again, creating a new binop continuation in the stack, saving the second expression, as before.

Expression DAG
Continuation DAG
$$ \rm{\small{Figure~8: Reduction~step~3}} $$

Expression DAG
Continuation DAG
$$ \rm{\small{Figure~9: Reduction~step~4}} $$
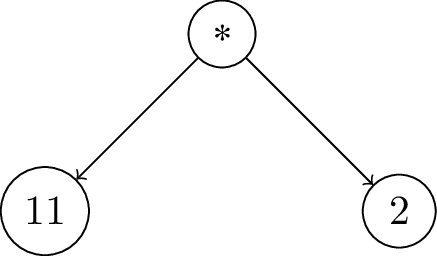
Expression DAG
Continuation DAG
$$ \rm{\small{Figure~10: Reduction~step~5}} $$
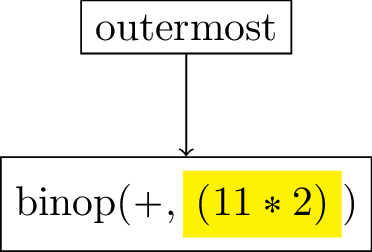
Now we have reached a point where the first argument of the binary operation is a self-evaluated expression: the number 4. We can then proceed by applying the continuation, which is responsible for removing itself from the continuation stack. I.e. the leaf binop continuation is removed and replaced with a binop2 continuation that will be applied when the second argument is evaluated. As a result, a thunk containing the evaluations of both arguments is created, such that the binary operation can finally be applied. We then return the control flow to the saved continuation, which is represented here as the previous continuation in the stack.
Since the result of the binary operation is the number 20, which is a self-evaluated expression, we can apply the continuation of the addition expression, creating a corresponding binop2.
Now we evaluate both input arguments of the first multiplication, producing a thunk containing all the information we need to proceed. For instance, we create a binop2 continuation containing the result 20.

Expression DAG
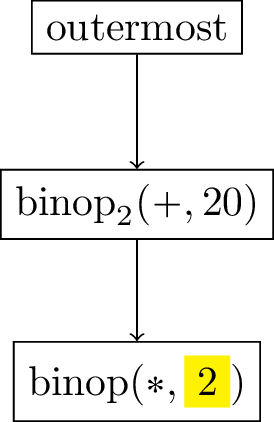
Continuation DAG
$$ \rm{\small{Figure~11: Reduction~step~6}} $$

Expression DAG
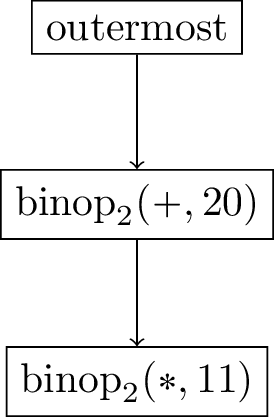
Continuation DAG
$$ \rm{\small{Figure~12: Reduction~step~7}} $$

Expression DAG
Continuation DAG
$$ \rm{\small{Figure~13: Reduction~step~8}} $$
Similarly, we evaluate the second multiplication following the same steps. Next, we evaluate the number 2, which is the first argument, and save the number 11 for the next reduction step.
Next, we evaluate the number 11, the second argument, and create a thunk to finish the calculation.
The thunk returns 42 as the result of the addition of 20 and 22 to the previous continuation, which is the outermost continuation. Therefore we simply replace it by the terminal continuation and finish the execution.
Environment #
The environment is a data structure that contains pairs of variables and values, such that the variables of Lurk expressions can be evaluated. This simply means that variables are replaced by their values.
Next we show a LET expression, which allows us to create variables in the environment. Briefly, a LET expression receives as input argument a list of pairs (variable, value), and a body, which is an expression that will be evaluated right after the list of variables is inserted into the environment.

Expression DAG

Continuation DAG
$$ \rm{\small{Figure~14: Reduction~step~9}} $$
> (let ((a 1)) a)
INFO lurk::eval > Frame: 0
Expr: (LET ((A 1)) A)
Env: NIL
Cont: Outermost
INFO lurk::eval > Frame: 1
Expr: 1
Env: NIL
Cont: Let{ var: A, body: A, saved_env: NIL, continuation: Outermost }
INFO lurk::eval > Frame: 2
Expr: A
Env: ((A . 1))
Cont: Tail{ saved_env: NIL, continuation: Outermost }
INFO lurk::eval > Frame: 3
Expr: 1
Env: NIL
Cont: Terminal
[3 iterations] => 1
$$ \rm{\small{Figure~15: LET~example}} $$
Store implementation #
In this section, we explain how the store is implemented in Lurk. Although the store is not essential to constructing the circuit, understanding its implementation is useful because the circuit must have components that behave equivalently. We replace the store implementation with corresponding mechanisms in the circuit to preserve the same properties. It is important to note that the underlying hash functions used in the store and the circuit are completely different, and there is no connection between the hash maps used in the store implementation and the use of Poseidon in the circuit.
The store is a set of pointers that uses hash maps to implement content-addressable storage. These maps allow us to insert pointers in the set in constant time. A distinct set is created for each pointer tag, including continuation pointers. When a new pointer is created, its content is inserted into the set, and an index is generated. This index is used as a raw pointer, which is useful for accessing the content later.
The following are the sets defined in the Lurk store: cons, comm, fun, sym, num, str, thunk, call, call, call2, tail, lookup, unop, binop, binop2, if, let, letrec, and emit. The store provides a convenient interface to create and access its content, such as the get and intern functions for each set.
An opaque pointer has a negative raw pointer, therefore it can’t be used as an index in the store. Hence such pointers do not have known content.
How to implement the store in the circuit:
Instead of using hash maps, the circuit uses non-determinism to construct cryptographic hash relations in the form y = H(x), where before starting the construction of the circuit, the prover already knows both the preimage, x, and the result, y, of the hash function. In the circuit, the prover shows all the intermediate steps necessary to calculate y from x. Hence, Lurk objects are represented as a Merkle-DAG, where arrows are constructed using this one-way hash function. To show that a certain path in the Merkle-DAG is valid, we non-deterministically provide the sequence of hash relations that corresponds to the needed witness (instead of indexing the hash maps, as we did in the store implementation). The prover can still use the hash map to efficiently build the witness, but from the perspective of the verifier, there is no store.
Note In the context of zero-knowledge proofs, non-determinism refers to the use of non-deterministic auxiliary inputs to improve the efficiency of the verification process. While computing the value of a function can be computationally expensive, verifying whether an already computed answer is correct is typically less costly. Provers can use non-deterministic auxiliary inputs to provide additional information, but high-level programs that compute the answer often lack this information. The benefits of non-determinism can be illustrated with the example of deciding whether two n-element lists are sorted copies of each other. For more on non-determinism, see 16
Poseidon #
Poseidon 14 is a hash function tailored for zero-knowledge proofs. Its input is a list of finite field elements, with the output given as a single field element. It is designed in a modular way, being appropriate in different scenarios, from Fiat-Shamir implementation to authenticated encryption [^SAFE].
Here we use it as a hash function to construct pointers, allowing us to have not only content addressable storage, but also a clean solution for recursion, since pointers can be used to represent expressions that contain other expressions in a natural way.
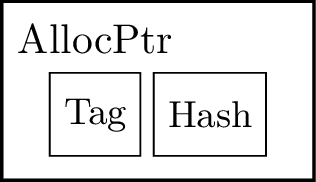
Figure 16: Allocated pointer

Figure 17: Hash preimage
Poseidon circuit #
Neptune 17 is a rust implementation of Poseidon, which allows efficient proof construction. In particular, the total number of constraints is 286 for the 4-ary instantiation, 334 for the 6-ary instantiation, and 385 for the 8-ary instantiation
Pointers in the circuit #
While pointers are implemented outside the circuit using dictionaries, we need a different solution for zero-knowledge circuits. One solution is to use hash functions as for example occurs in the construction of Merkle Trees. Poseidon hash function is allegedly a good solution for Lurk pointers, since it can be implemented using a small number of R1CS constraints.
As shown previously, each possible expression or continuation can be represented using at most 8 field elements. Therefore, we designed the system to allow the hash preimage to be formed by at most 4 components, as shown in Figure 17
Next, we describe in detail how we construct pointers in the circuit. In summary, a cons operation requires the 4-ary hash, functions require the 6-ary hash, and generic pointers require 8-ary hash.
- Let $a = \gad{CONSTRUCT}(\var{cont-tag}, \var{components})$:
- Call $\var{hash} = \gad{POSEIDON}(\var{components})$ - using the 8-ary hash.
- Return $\var{ALLOC-PTR}(\var{cont-tag}, \var{hash})$.
- Let $\gad{CONSTRUCT-CONS}(\var{car}, \var{cdr})$:
- Let $\var{hash} = \gad{POSEIDON}(\var{car}, \var{cdr})$, using the 4-ary hash.
- Return $\gad{ALLOC-PTR}(\var{globals.cons-tag}, \var{hash})$.
- Let $\gad{CONSTRUCT-FUN}(\var{arg}, \var{body}, \var{closed-env})$:
- Call $\var{hash} = \gad{POSEIDON}(\var{arg}, \var{body}, \var{closed})$, using the 6-ary hash.
- Return $\gad{ALLOC-PTR}(\var{globals.fun-tag}, \var{hash})$.
- Let $\gad{CONSTRUCT-LIST}(\var{elts})$:
- Let $\var{first} = \var{elts}[0]$.
- Let $\var{rest-of-elts} = \var{elts}[1.~.~]$.
- Call $\var{tail} = \gad{CONSTRUCT-LIST}(\var{rest-of-elts})$.
- Return $\gad{CONSTRUCT-CONS}(\var{first}, \var{tail})$.
- Let $\gad{CONSTRUCT-THUNK}(\var{val}, \var{cont})$:
Error system #
Lurk programs can generate error continuations, which indicate an unrecoverable situation. This error is used to finalize the computation. Therefore, it is possible to construct zero-knowledge proofs that a program generated this error. It is important to remark that the error doesn’t carry detailed information to identify the cause of the error. The error can happen for malformed programs, like unary operations that receive more than one argument, or binary operations that receive fewer than two arguments. It can also happen if someone tries to divide by zero. However, the zero-knowledge proofs do not reveal which kind of error occurred.
As an example, when we try to divide by zero, the final output continuation is Error, which is a global pointer used instead of Terminal, such that a verifier can recognize that this program didn’t finish successfully.
> (/ 42 0)
INFO lurk::eval > Frame: 0 Expr: (/ 42 0)
Env: NIL
Cont: Outermost
INFO lurk::eval > Frame: 1 Expr: 42
Env: NIL
Cont: Binop{ operator: Quotient, unevaled_args: (0), saved_env: NIL, continuation: Outermost }
INFO lurk::eval > Frame: 2 Expr: 0
Env: NIL
Cont: Binop2{ operator: Quotient, evaled_arg: 42, continuation: Outermost }
INFO lurk::eval > Frame: 3 Expr: 0
Env: NIL
Cont: Error
$$ \rm{\small{Figure~18: Error~example}} $$
High-level algorithms #
Now we can start to describe how Lurk programs are translated into R1CS constraints. The strategy is to follow a top-down approach, by first showing some high-level components and saying how they interact. Later we can present the low-level construction of constraints.
Self-evaluated expressions:
Some expressions already are in the final stage of evaluation (as, for example, literal expressions like NIL, literal numbers, and characters). The complete list of self-evaluated expressions is given by the following tags: nil, num, fun, char, str, comm.
Unary expressions: As the name suggests, unary expressions correspond to operations that receive only one input argument, which in Lurk are given by expressions that must be evaluated before the unary operation is evaluated.
atom. It returns $\tt{\footnotesize{true}}$ if and only if the input argument is not a list.car. This operation receives as input a list and returns its first element.cdr. Complementary to the previous item, it receives a list and returns everything except for the first element.emit. This operation emits an intermediary output expression, so that it can be externally viewed.commit. Creates a commitment to the received expression.open. It is used to open a commitment.secret. It returns the secret element used to create a given commitment.num. Interprets the finite field element as a number.u64. Interprets the finite field element as a 64-bit unsigned integer.comm. Interprets the finite field element as a commitment.char. Interprets the finite field element as a character.
Below is example of a unary expression evaluation.
> (atom 42)
INFO lurk::eval > Frame: 0 Expr: (ATOM 42)
Env: NIL
Cont: Outermost
INFO lurk::eval > Frame: 1 Expr: 42
Env: NIL
Cont: Unop{ operator: Atom, continuation: Outermost }
INFO lurk::eval > Frame: 2 Expr: T
Env: NIL
Cont: Terminal
$$ \rm{\small{Figure~19: Unary~operation~example}} $$
As a first step, a unop continuation is created, pointing to the outermost continuation. Since 42 is a self-evaluated expression, we can continue the evaluation of this continuation, by returning T.
Binary expressions:
+. Addition of the received elements.-. Subtraction of the received elements.*. Multiplication of the received elements./. Division of the received elements.%. Modular reduction of received elements.>. Greater than.>=. Greater than or equal.>. Less than.<=. Less than or equal.=. Equality test between numbers.eq. Equality test between pointers.cons. Creates a list formed by the concatenation of the received elements.strcons. Creates a list formed by the concatenation of acharand astring.begin. Allows evaluation of multiple expressions, returning the result of the last one.hide. Uses the first argument as a secret to create a commitment to the second argument.
Here is an example showing how Lurk evaluates an addition:
> (+ 2 40)
INFO lurk::eval > Frame: 0 Expr: (+ 2 40)
Env: NIL
Cont: Outermost
INFO lurk::eval > Frame: 1 Expr: 2
Env: NIL
Cont: Binop{ operator: Sum, unevaled_args: (40), saved_env: NIL, continuation: Outermost }
INFO lurk::eval > Frame: 2 Expr: 40
Env: NIL
Cont: Binop2{ operator: Sum, evaled_arg: 2, continuation: Outermost }
INFO lurk::eval > Frame: 3 Expr: 42
Env: NIL
Cont: Terminal
[3 iterations] => 42
$$ \rm{\small{Figure~20: Binary~operation~example}} $$
The addition expression is reduced by creating a binop continuation containing the second input argument. The first argument is a self-evaluated expression, after which we can create a binop2 continuation, where the second argument will be evaluated, and the sum of both results is returned as a terminal continuation.
Equality expressions:
Equality operators are binary operations, therefore we have binop and binop2 continuations.
=. Used to check equality of numbers.eq. Used to check equality of pointers.
Comparison expressions:
>. Greater than operation.>=. Greater than or equal operation.<. Less than operation.<=. Less than or equal operation.
Conditional expression:
if. Receives 3 expressions as arguments. If the first one evaluates to something different fromnil, then the result is given by the evaluation of the second expression. Otherwise, the result is the evaluation of the third one.
Functional commitments #
General work related to functional commitments can be found here 18 19 20.
Functional commitments having a function-privacy property, specifically, are described in this paper 21. We implement functional commitments as first-class Lurk operations. Specifically, we use cons in order to compute the hash of a function and a secret number. Later, we can prove this function evaluates to determined values. In order to construct functional commitments, we need some building blocks, which Lurk provides natively, and whose high-level description is the following:
- hide(secret, maybe-payload)
- If there aren't exactly 2 input arguments, return error.
- Otherwise, compute the commitment using all arguments as input of a 3-ary Poseidon instance.
- Allocate a pointer to it.
- Return this pointer.
- commit(payload)
- If there isn’t exactly 1 input argument, return error.
- Otherwise, compute the commitment, using zero as the value of the secret.
- Allocate a pointer to it.
- Return this pointer.
- open(commitment)
- If there isn’t exactly 1 input argument, return error.
- Otherwise, if the commitment is known, find the corresponding pair (secret, payload).
- Allocate a pointer to the payload.
- Return this pointer.
- secret(commitment)
- If there isn’t exactly 1 input argument, return error.
- Otherwise, if the commitment is known, find the corresponding pair (secret, payload).
- Allocate a pointer to the secret.
- Return this pointer.
- comm(value)
- Take as input a pointer to the value, and it finds the field element given by value.hash().
- Allocate a pointer whose tag is globals.comm-tag and the hash is given value.hash().
- Return this pointer.
The commitment scheme is implemented by concatenating a pointer and a secret field element and computing the Poseidon hash function. Since functions are defined using lambda expressions, we obtain functional commitments basically for free.
Globals #
We allocate constants in order to represent global data. For instance, we have global pointers, such as the terminal pointer, which can only be used in the last frame to indicate a program finished successfully. We also have an error pointer for programs that didn’t finish correctly. The first frame determines the outermost continuation, which has an outermost continuation pointer. Another important global pointer is the one that points to the symbol nil.
We also have global constants for each different tag in the system. Those constants are useful for comparing runtime data and determining which kind of pointer we are dealing with.
Beyond that, we have constants for Boolean variables. We pair $\tt{\footnotesize{true}}$ with 1 and $\tt{\footnotesize{false}}$ with 0. Finally, we have a constant of value 0 for default numbers.
Reduce expression #
In this section, we explain the step-by-step reduction of complex expressions.
First, we provide an overview in Algorithm 3.1, which constructs multicase clauses selected based on the expression tag. Each distinct tag has a different reduction method, but the overall process remains the same. The result of the reduction provides a new triple of expression, environment, and continuation. Additionally, it determines whether we need to apply the continuation, resulting in a new IO consisting of the triple expression, environment, and continuation. For certain continuations, we need to create a thunk.
Reducing self-evaluated expressions is straightforward. The expression, environment, and continuation remain unchanged, but we must apply the continuation to the evaluated expression.
If the expression is a thunk, we need to verify hash consistency before applying the continuation.
If the expression is a symbol or a cons, we have two distinct scenarios that require detailed explanations. Therefore, we will dedicate a section to each scenario.
$ \cirtitle{Circuit~3.1}~\cir{Reduce-Expression} \\ $
$ \cirio{INPUT} \var{expr},\var{env},\var{cont},\var{not-dummy},\var{witness}, \var{allocated-cons-witness}, \var{allocated-cont-witness}$.
$ \cirio{OUTPUT} \var{expr},\var{env},\var{cont}$.
- $\com{Compute and add clauses for self-evaluated expressions.}$
- $\com{Compute and add thunk clause.}$
- $\com{Compute and add sym clause.}$
- $\com{Compute and add cons clause.}$
- $\com{Get result from multicase gadget.}$
- $\com{Apply continuation.}$
- $\com{Make thunk.}$
- $\com{Error handling.}$
- Return $(\var{expr}, \var{env}, \var{cont})$.
Specifically, we do the following:
- Let $\var{clauses} = \gad{MULTICASE-CLAUSES}()$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.nil},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.num},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.fun},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.char},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.str},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.comm},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.key},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.u64},\var{expr},\var{env},\var{cont},\var{witness},\var{globals})$.
- Let $\var{cont-is-terminal} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.terminal-tag}())$.
- Let $\var{cont-is-error} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.error-tag}())$.
- Let $\var{expr-is-thunk} = \gad{ALLOC-TAG-EQUAL}(\var{expr.tag}(), \var{globals.thunk-tag})$.
- Let $(\var{expr-thunk-hash}, \var{expr-thunk-value}, \var{expr-thunk-continuation}) = \var{expr}.\gad{ALLOCATE-THUNK-COMPONENTS-UNCONSTRAINED}()$.
- Call $\gad{IMPLIES-EQUAL}(\var{expr-is-thunk}, \var{expr-thunk-hash}, \var{expr.hash}())$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.thunk}, \var{expr-thunk-value}, \var{env}, \var{expr-thunk-continuation}, \var{globals.true-num})$.
- Let $\var{reduce-sym-not-dummy} = \gad{ALLOC-TAG-EQUAL}(\var{expr.tag}(), \var{globals.sym-tag})$.
- Let $\var{cont-is-terminal-or-error} = \gad{OR}(\var{cont-is-terminal}, \var{cont-is-error})$.
- Let $\var{cont-is-not-terminal-or-error} = \var{cont-is-terminal-or-error}.\gad{NOT}()$.
- Let $\var{reduce-sym-not-dummy} = \gad{AND}(\var{reduce-sym-not-dummy}, \var{cont-is-not-terminal-or-error})$.
- Let $(\var{result}, \var{sym-env}, \var{sym-cont}, \var{sym-apply-cont}) = \cir{Reduce-Sym}(\var{expr}, \var{env}, \var{cont}, \var{reduce-sym-not-dummy}, \var{witness}, \var{allocated-cons-witness}, \var{allocated-cont-witness})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.sym}, \var{sym-result}, \var{sym-env}, \var{sym-cont}, \var{sym-apply-cont})$.
- Let $\var{expr-is-cons} = \gad{ALLOC-TAG-EQUAL}(\var{expr.tag}(), \var{globals.cons-tag})$.
- Let $\var{reduce-cons-not-dummy} = \gad{AND}(\var{expr-is-cons}, \var{cont-is-not-terminal-or-error})$.
- Let $(\var{cons-result}, \var{cons-env}, \var{cons-cont}, \var{cons-apply-cont}) = \var{Reduce-cons}(\var{expr}, \var{env}, \var{cont}, \var{reduce-cons-not-dummy}, \var{witness}, \var{allocated-cons-witness}, \var{allocated-cont-witness})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{tag.cons}, \var{cons-result}, \var{cons-env}, \var{cons-cont}, \var{cons-apply-cont})$.
- Let $\var{results} = \var{MULTICASE}(\var{expr.tag}(), \var{clauses})$.
- Let $\var{first-result-expr0} = \var{results}[0])$.
- Let $\var{first-result-expr} = \var{PICK}(\var{cont-is-terminal-or-error}, \var{globals.nil-ptr}, \var{first-result-expr0})$.
- Let $\var{first-result-env} = \var{results}[1]$.
- Let $\var{first-result-cont} = \var{results}[2]$.
- Let $\var{first-result-apply-continuation} = \var{results}[6]$.
- Let $\var{apply-continuation-boolean0} = \gad{ALLOC-IS-ZERO}(\var{first-result-apply-continuation}).\gad{NOT}()$.
- Let $\var{apply-continuation-boolean} = \gad{AND}(\var{apply-continuation-boolean0}, \var{cont-is-not-terminal-or-error})$.
- Let $\var{apply-continuation-results}=\cir{Apply-Continuation}(\var{expr},\var{env},\var{cont},\var{witness},\var{globals},\var{flag})$.
- Let $\var{apply-continuation-make-thunk} = \var{apply-continuation-results}[3]$.
- Let $\var{result-expr0} = \gad{PICK}(\var{apply-continuation-boolean}, \var{apply-continuation-results}[0], \var{first-result-expr})$.
- Let $\var{result-env0} = \gad{PICK}(\var{apply-continuation-boolean}, \var{apply-continuation-results}[1], \var{first-result-env})$.
- Let $\var{result-cont0} = \gad{PICK}(\var{apply-continuation-boolean}, \var{apply-continuation-results}[2], \var{first-result-cont})$.
- Let $\var{make-thunk-num} = \gad{PICK}(\var{apply-continuation-boolean}, \var{apply-continuation-make-thunk}, \var{globals.false-num})$.
- Let $\var{make-thunk-boolean} = \gad{ALLOC-IS-ZERO}(\var{make-thunk-num}).\gad{NOT}()$.
- Let $\var{thunk-results} = \cir{Make-Thunk}(\var{result-cont0}, \var{result-expr0}, \var{result-env0}, \var{make-thunk-boolean}, \var{allocated-cont-witness})$.
- Let $\var{result-expr-candidate} = \gad{PICK}(\var{make-thunk-boolean}, \var{thunk-results}[0], \var{result-expr0})$.
- Let $\var{result-env-candidate} = \gad{PICK}(\var{make-thunk-boolean}, \var{thunk-results}[1], \var{result-env0})$.
- Let $\var{result-cont-candidate} = \gad{PICK}(\var{make-thunk-boolean}, \var{thunk-results}[2], \var{result-cont0})$.
- Let $\var{result-expr} = \gad{PICK}(\var{cont-is-terminal-or-error}, \var{expr}, \var{result-expr-candidate})$.
- Let $\var{result-env} = \gad{PICK}(\var{cont-is-terminal-or-error}, \var{env}, \var{result-env-candidate})$.
- Let $\var{result-cont} = \gad{PICK}(\var{cont-is-terminal-or-error}, \var{cont}, \var{result-cont-candidate})$.
- Return $(\var{result-expr}, \var{result-env}, \var{result-cont})$.
Reduce symbol #
To reduce symbol expressions, we must determine whether the symbol is a self-evaluated symbol or a variable that needs to be looked up in the environment. If it’s the latter, we must determine whether we have a regular or recursive environment. In a regular environment, we compare the given symbol with the first binding in the environment. If it’s the variable we’re looking for, we return the corresponding value in a thunk. Otherwise, we recursively call the lookup method in the remaining bindings in the environment. For a recursive environment, we follow the same strategy, but using closures when the value to be used is a function.
To carry out these steps, we first analyze whether the expression is a self-evaluated symbol, like NIL or T, or a variable name that we must look up in the environment. Distinguishing between these possibilities requires multiple booleans and using car-cdr to split the expression and environment in a way that lets us identify code paths leading to the end of the recursive lookup or error continuations.
Finally, we compute a boolean that identifies the control flow. In other words, we determine whether to apply the continuation or not. This boolean is crucial because we must always run the part of the circuit corresponding to apply_cont(), but we restrict the circuit to use dummy variables when this boolean value is false.
$ \cirtitle{Circuit~3.2}~\cir{Reduce-Sym} \\ $
$ \cirio{INPUT} \var{expr},\var{env},\var{cont},\var{not-dummy},\var{witness}, \var{allocated-cons-witness}, \var{allocated-cont-witness}$.
$ \cirio{OUTPUT} \var{expr},\var{env},\var{cont}$.
- $\com{Calculate condition terms.}$
- $\com{Calculate output predicate.}$
- $\com{Calculate conditions.}$
- $\com{Calculate implications.}$
The algorithm receives as input a triple $(\var{expr}, \var{env}, \var{cont})$, together with a variable called $\var{not-dummy}$, which is a Boolean whose value is false when the input expression is not a symbol. In this case, $\cir{Reduce-Sym}$ constraints are not actually used, which means those constraints will contain only dummy values. The algorithm also receives the witness, the store, and the globals as input.
The circuit described here mimics the evaluation of expressions whose tag is equal to $\var{globals.sym-tag}$. However, if we follow exactly the same steps as implemented in eval.rs, then some constraints would be unnecessarily repeated. Hence, in order to eliminate those constraints, we need to pay the price of making it a bit harder to guarantee that the circuit implementation corresponds to what is implemented in eval.rs. We clarify here the differences between both worlds, and show why they are equivalent.
- Circuit Reduce-Symbol( expr: AllocatedPtr, env: AllocatedPtr, cont: AllocatedPtr, not_dummy: Boolean, witness: Witness ):
- Calculate condition terms:
- Let $\var{output-expr} = \var{witness}.\var{prethunk-output-expr}$.
- Let $\var{output-env} = \var{witness}.\var{prethunk-output-env}$.
- Let $\var{output-cont} = \var{witness}.\var{prethunk-output-cont}$.
- Let $\var{sym-is-nil} = \var{expr}.\gad{IS-NIL}()$.
- Let $\var{sym-is-t} = \gad{ALLOC-EQUAL}(\var{expr}, \var{globals.t-ptr})$.
- Let $\var{sym-is-nil-or-t} = \gad{OR}(\var{sym-is-nil}, \var{sym-is-t})$.
- Let $\var{sym-is-self-evaluating} = \gad{AND}(\var{sym-is-nil-or-t}, \var{not-dummy})$.
- Let $\var{sym-otherwise} = \gad{AND}(\var{sym-is-self-evaluating}.\gad{NOT}(), \var{not-dummy})$.
- Let $\var{env-is-nil} = \var{env}.\gad{IS-NIL}()$
- Let $\var{env-not-nil} = \var{env-is-nil}.\gad{NOT}()$.
- Let $\var{env-not-dummy} = \var{sym-otherwise}$.
- Let $(\var{binding}, \var{smaller-env}) = \gad{CAR-CDR-NAMED}(\var{env}, \var{names.env}, \var{allocated-cons-witness}, \var{env-not-dummy})$.
- Let $\var{main} = \gad{AND}(\var{sym-otherwise}, \var{env-not-nil})$.
- Let $\var{binding-is-nil} = \var{binding}.\gad{IS-NIL}()$.
- Let $\var{binding-not-nil} = \var{binding-is-nil}.\gad{NOT}()$.
- Let $\var{binding-is-cons} = \gad{IS-CONS}(\var{binding})$.
- Let $\var{env-car-not-dummy} = \gad{AND}(\var{main}, \var{binding-is-cons})$.
- Let $(\var{var-or-rec-binding}, \var{val-or-more-rec-env}) = \gad{CAR-CDR-NAMED}(\var{binding}, \var{names.env-car}, \var{allocated-cons-witness}, \var{env-car-not-dummy})$.
- Let $\var{var-or-rec-binding-is-sym} = \gad{IS-SYM}(\var{var-or-rec-binding})$.
- Let $\var{var-or-rec-binding-is-cons} = \gad{IS-CONS}(\var{var-or-rec-binding})$.
- Let $\var{var-or-rec-binding-is-sym-or-cons} = \gad{OR}(\var{var-or-rec-binding-is-sym}, \var{var-or-rec-binding-is-cons})$.
- Let $\var{with-binding} = \gad{AND}(\var{main}, \var{binding-not-nil})$.
- Let $\var{with-sym-binding} = \gad{AND}(\var{with-binding}, \var{var-or-rec-binding-is-sym})$.
- Let $\var{with-cons-binding} = \gad{AND}(\var{with-binding}, \var{var-or-rec-binding-is-cons})$.
- Let $\var{with-other-binding} = \gad{AND}(\var{with-binding}, \var{var-or-rec-binding-is-sym-or-cons}.\gad{NOT}())$.
- Let $v = \var{var-or-rec-binding}$.
- Let $\var{val} = \var{val-or-more-rec-env}$.
- Let $\var{v-is-expr1} = \gad{ALLOC-EQUAL}(\var{expr}, v)$.
- Let $\var{envcaar-not-dummy} = \var{with-cons-binding}$.
- Let $(\var{v2}, \var{val2}) = \gad{CAR-CDR-NAMED}(\var{globals}, \var{var-or-rec-binding}, \var{names.env-caar}, \var{allocated-cons-witness}, \var{envcaar-not-dummy})$.
- Let $\var{val2-is-fun} = \gad{IS-FUN}(\var{val2})$.
- Let $\var{v2-is-expr} = \gad{ALLOC-EQUAL}(\var{v2}, \var{expr})$.
- Let $\var{v2-is-expr-real} = \gad{AND}(\var{v2-is-expr}, \var{envcaar-not-dummy})$.
- Let $\var{extended-env-not-dummy} = \gad{AND}(\var{val2-is-fun}, \var{v2-is-expr-real})$.
- Let $(\var{fun-hash}, \var{fun-arg}, \var{fun-body}, \var{fun-closed-env}) = \gad{ALLOCATE-MAYBE-FUN-UNCONSTRAINED}(\var{witness}.\fun{closure-to-extend}())$.
- Call $\gad{IMPLIES-EQUAL}(\var{extended-env-not-dummy}, \var{fun-hash}, \var{val2.hash}())$.
- Let $\var{rec-env} = \var{binding}$.
- Let $\var{extended-env} = \gad{CONSTRUCT-CONS-NAMED}(\var{rec-env}, \var{fun-closed-env}, \var{names.extended-closure-env}, \var{allocated-cons-witness}, \var{extended-env-not-dummy})$.
- Let $\var{extended-fun} = \gad{CONSTRUCT-FUN}(\var{fun-arg}, \var{fun-body}, \var{extended-env})$.
- Let $\var{val-to-use} = \gad{PICK}(\var{val2-is-fun}, \var{extended-fun}, \var{val2})$.
- Let $\var{smaller-rec-env} = \var{val-or-more-rec-env}$.
- Let $\var{smaller-rec-env-is-nil} = \var{smaller-rec-env}.\gad{IS-NIL}()$.
- Let $\var{smaller-rec-env-not-nil} = \var{smaller-rec-env-is-nil}.\gad{NOT}()$.
- Let $\var{v2-not-expr} = \var{v2-is-expr}.\gad{NOT}()$.
- Let $\var{otherwise-and-v2-not-expr} = \gad{AND}(\var{v2-not-expr}, \var{with-cons-binding})$.
- Let $\var{smaller-rec-env-not-dummy} = \gad{AND}(\var{smaller-rec-env-not-nil}, \var{otherwise-and-v2-not-expr})$.
- Let $\var{rec-extended-env} = \gad{CONSTRUCT-CONS-NAMED}(\var{smaller-rec-env}, \var{smaller-env}, \var{names.env-to-use}, \var{allocated-cons-witness}, \var{smaller-rec-env-not-dummy})$.
- Let $\var{env-to-use} = \gad{PICK}(\var{smaller-rec-env-is-nil}, \var{smaller-env}, \var{rec-extended-env})$.
- Let $\var{cont-is-lookup} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.lookup-cont-tag}$.
- Let $\var{needed-env-missing} = \gad{AND}(\var{sym-otherwise}, \var{env-is-nil})$.
- Let $\var{needed-binding-missing} = \gad{AND}(\var{main}, \var{binding-is-nil})$.
- Let $\var{with-sym-binding-matched} = \gad{AND}(\var{with-sym-binding}, \var{v-is-expr1})$.
- Let $\var{with-sym-binding-unmatched} = \gad{AND}(\var{with-sym-binding}, \var{v-is-expr1}.\gad{NOT}())$.
- Let $\var{with-sym-binding-unmatched-old-lookup} = \gad{AND}(\var{with-sym-binding-unmatched}, \var{cont-is-lookup})$.
- Let $\var{with-sym-binding-unmatched-new-lookup} = \gad{AND}(\var{with-sym-binding-unmatched}, \var{cont-is-lookup}.\gad{NOT}())$.
- Let $\var{with-cons-binding-matched} = \gad{AND}(\var{with-cons-binding}, \var{v2-is-expr})$.
- Let $\var{with-cons-binding-unmatched} = \gad{AND}(\var{with-cons-binding}, \var{v2-is-expr}.\gad{NOT}())$.
- Let $\var{with-cons-binding-unmatched-old-lookup} = \gad{AND}(\var{with-cons-binding-unmatched}, \var{cont-is-lookup})$.
- Let $\var{with-cons-binding-unmatched-new-lookup} = \gad{AND}(\var{with-cons-binding-unmatched}, \var{cont-is-lookup}.\gad{NOT}())$.
- Let $\var{lookup-continuation-not-dummy} = \gad{OR}(\var{with-sym-binding-unmatched-new-lookup}, \var{with-cons-binding-unmatched-new-lookup})$.
- Let $\var{lookup-continuation} = \gad{CONSTRUCT-NAMED}(\var{names.lookup}, \var{globals.lookup-cont-tag}, (\var{env}, \var{cont}, \var{default-num-pair}, \var{default-num-pair}), \var{allocated-cont-witness}, \var{lookup-continuation-not-dummy})$.
- Calculate output predicate:
- Let$\var{output-expr-is-expr} = \gad{EQUAL}(\var{output-expr}, \var{expr})$.
- Let $\var{output-env-is-env} = \gad{EQUAL}(\var{output-env}, \var{env})$.
- Let $\var{output-cont-is-cont} = \gad{EQUAL}(\var{output-cont}, \var{cont})$.
- Let $\var{output-cont-is-error} = \gad{EQUAL}(\var{output-cont}, \var{globals.error-ptr})$.
- Let $\var{output-expr-is-val} = \var{EQUAL}(\var{output-expr}, \var{val})$.
- Let $\var{output-env-is-smaller-env} = \gad{EQUAL}(\var{output-env}, \var{smaller-env})$.
- Let $\var{output-cont-is-lookup} = \gad{EQUAL}(\var{output-cont}, \var{lookup-continuation})$.
- Let $\var{output-expr-is-val-to-use} = \gad{EQUAL}(\var{output-expr}, \var{val-to-use})$.
- Let $\var{output-env-is-env-to-use} = \gad{EQUAL}(\var{output-env}, \var{env-to-use})$.
- Calculate conditions:
- Let $\var{output-expr-should-be-expr} = \gad{OR}(\var{needed-env-missing}, \var{sym-is-self-evaluating}, \var{needed-binding-missing}, \var{with-sym-binding-unmatched}, \var{with-cons-binding-unmatched})$.
- Let $\var{output-expr-should-be-val} = \var{with-sym-binding-matched}$.
- Let $\var{output-expr-should-be-val-to-use} = \var{with-cons-binding-matched}$.
- Let $\var{output-env-should-be-env} = \gad{OR}(\var{needed-binding-missing}, \var{needed-env-missing}, \var{sym-is-self-evaluating}, \var{with-sym-binding-matched}, \var{with-cons-binding-matched})$.
- Let $\var{output-env-should-be-smaller-env} = \var{with-sym-binding-unmatched}$.
- Let $\var{output-env-should-be-env-to-use} = \var{with-cons-binding-unmatched-new-lookup}$.
- Let $\var{output-cont-should-be-cont} = \gad{OR}(\var{sym-is-self-evaluating}, \var{with-sym-binding-matched}, \var{with-sym-binding-unmatched-old-lookup}, \var{with-cons-binding-matched}, \var{with-cons-binding-unmatched-old-lookup})$.
- Let $\var{output-cont-should-be-error} = \gad{OR}(\var{with-other-binding}, \var{needed-env-missing}, \var{needed-binding-missing})$.
- Calculate implications:
- Call $\gad{IMPLIES}(\var{output-expr-should-be-expr}, \var{output-expr-is-expr})$.
- Call $\gad{IMPLIES}(\var{output-expr-should-be-val}, \var{output-expr-is-val})$.
- Call $\gad{IMPLIES}(\var{output-expr-should-be-val-to-use}, \var{output-expr-is-val-to-use})$.
- Call $\gad{IMPLIES}(\var{output-cont-should-be-error}, \var{output-expr-is-expr})$.
- Call $\gad{IMPLIES}(\var{output-env-should-be-env}, \var{output-env-is-env})$.
- Call $\gad{IMPLIES}(\var{output-env-should-be-smaller-env}, \var{output-env-is-smaller-env})$.
- Call $\gad{IMPLIES}(\var{output-env-should-be-env-to-use}, \var{output-env-is-env-to-use})$.
- Call $\gad{IMPLIES}(\var{output-cont-should-be-error}, \var{output-env-is-env})$.
- Call $\gad{IMPLIES}(\var{output-cont-should-be-cont}, \var{output-cont-is-cont})$.
- Call $\gad{IMPLIES}(\var{output-cont-should-be-error}, \var{output-cont-is-error})$.
- Call $\gad{IMPLIES}(\var{lookup-continuation-not-dummy}, \var{output-cont-is-lookup})$.
- Let $\var{apply-cont-bool} = \gad{OR}(\var{with-cons-binding-matched}, \var{with-sym-binding-matched}, \var{sym-is-self-evaluating})$.
- Let $\var{apply-cont-num} = \gad{BOOLEAN-NUM}(\var{apply-cont-bool})$.
- Return $(\var{output-expr}, \var{output-env}, \var{output-cont}, \var{apply-cont-num})$.
Reduce Cons #
In this section we describe the $\cir{Reduce-Cons}()$ algorithm, which is responsible for taking a cons expression and reducing it to a triple (expr, env, cont) to be evaluated next, and determining if the continuation will be applied or not.
In order to avoid calculating unnecessary hashes inside the circuit, we first use a multicase to select the preimage for the next continuation, then we compute – just once – the continuation pointer. Afterward, we use a second multicase to select the final result.
$ \cirtitle{Circuit~3.3}~\cir{Reduce-cons} \\ $
- $\cirio{INPUT} \var{expr}, \var{env}, \var{cont}, \var{witness}$.
- $\cirio{OUTPUT} \var{expr}, \var{env}, \var{cont}$.
- $\com{Compute preimage clauses.}$
- Let $\var{preimage} = \gad{MULTICASE}(\var{preimage-clauses})$.
- $\com{Calculate newer continuation pointer.}$
- $\com{Compute clauses.}$
- $\var{result} = \gad{MULTICASE}(\var{clauses})$.
- Return $\var{result}$.
In $\cir{Reduce-Sym}()$ we dealt with expressions that correspond to just one symbol. On the other hand, $\cir{Reduce-Cons}()$ allows us to reduce more complicated expressions, since a cons expression can represent unary and binary operations. In particular, those operations have a list of parameters that themselves can be symbols or cons expressions.
Here we can describe how to reduce cons expressions:
A $\tt{\footnotesize{cons}}$ expression can also be used to represent lambda, let, and letrec operations. The first thing we do with a cons operation is to split its arguments into head – the first element of the expression, which corresponds to the car operation – and the rest of the elements, which correspond to the cdr operation. Next, we describe how we calculate the constraints and how we add one clause to the multicase gadget for each possible head.
- Let $(\var{head}, \var{rest}) = \cir{CAR-CDR-NAMED}(\var{expr}, \var{cons-names.expr}, \var{allocated-cons-witness}, \var{not-dummy})$.
- Let $\var{head-is-lambda0} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.lambda-sym.hash}())$.
- Let $\var{head-is-let} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.let-sym.hash}())$.
- Let $\var{head-is-letrec} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.letrec-sym.hash}())$.
- Let $\var{head-is-eval} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.eval-sym.hash}())$.
- Let $\var{head-is-quote0} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.quote-sym.hash}())$.
- Let $\var{head-is-cons} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.cons-sym.hash}())$.
- Let $\var{head-is-hide} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.hide-sym.hash}())$.
- Let $\var{head-is-commit} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.commit-sym.hash}())$.
- Let $\var{head-is-open} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.open-sym.hash}())$.
- Let $\var{head-is-secret} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.secret-sym.hash}())$.
- Let $\var{head-is-num} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.num-sym.hash}())$.
- Let $\var{head-is-u64} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.u64-sym.hash}())$.
- Let $\var{head-is-comm} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.comm-sym.hash}())$.
- Let $\var{head-is-char} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.char-sym.hash}())$.
- Let $\var{head-is-begin} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.begin-sym.hash}())$.
- Let $\var{head-is-car} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.car-sym.hash}())$.
- Let $\var{head-is-cdr} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.cdr-sym.hash}())$.
- Let $\var{head-is-atom} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.atom-sym.hash}())$.
- Let $\var{head-is-emit} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.emit-sym.hash}())$.
- Let $\var{head-is-plus} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.plus-sym.hash}())$.
- Let $\var{head-is-minus} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.minus-sym.hash}())$.
- Let $\var{head-is-times} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.times-sym.hash}())$.
- Let $\var{head-is-div} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.div-sym.hash}())$.
- Let $\var{head-is-mod} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.mod-sym.hash}())$.
- Let $\var{head-is-numequal} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.numequal-sym.hash}())$.
- Let $\var{head-is-eq} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.eq-sym.hash}())$.
- Let $\var{head-is-less} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.less-sym.hash}())$.
- Let $\var{head-is-less-equal} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.less-equal-sym.hash}())$.
- Let $\var{head-is-greater} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.greater-sym.hash}())$.
- Let $\var{head-is-greater-equal} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.greater-equal-sym.hash}())$.
- Let $\var{head-is-if0} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.if-sym.hash}())$.
- Let $\var{head-is-current-env0} = \gad{ALLOC-EQUAL}(\var{head.hash}(), \var{globals.current-env-sym.hash}())$.
- Let $\var{head-is-a-sym} = \gad{IS-SYM}(\var{head})$.
- Let $\var{head-is-fun} = \gad{IS-FUN}(\var{head})$.
- Let $\var{head-is-a-cons} = \gad{IS-CONS}(\var{head})$.
- Let $\var{head-is-binop0} = \gad{OR}(\var{head-is-cons}, \var{head-is-strcons}, \var{head-is-hide}, \var{head-is-begin}, \var{head-is-plus}, \var{head-is-minus}, \var{head-is-times}, \var{head-is-div}, \\ \var{head-is-mod}, \var{head-is-equal}, \var{head-is-eq}, \var{head-is-less}, \var{head-is-less-equal}, \var{head-is-greater}, \var{head-is-greater-equal}, \var{head-is-if}, \var{head-is-eval})$.
- Let $\var{head-is-binop} = \gad{AND}(\var{head-is-binop0}, \var{head-is-a-sym})$.
- Let $\var{head-is-unop0} = \gad{OR}(\var{head-is-car}, \var{head-is-cdr}, \var{head-is-commit}, \var{head-is-num}, \var{head-is-u64}, \var{head-is-comm}, \var{head-is-char}, \var{head-is-open}, \var{head-is-secret}, \var{head-is-atom}, \var{head-is-emit}, \var{head-is-eval}$.
- Let $\var{head-is-let-or-letrec0} = \gad{OR}(\var{head-is-let}, \var{head-is-letrec})$.
- Let $\var{head-is-let-or-letrec} = \gad{AND}(\var{head-is-let-or-letrec0}, \var{head-is-a-sym})$.
- Let $\var{head-is-lambda} = \gad{AND}(\var{head-is-lambda0}, \var{head-is-a-sym})$.
- Let $\var{head-is-quote} = \gad{AND}(\var{head-is-quote0}, \var{head-is-a-sym})$.
- Let $\var{head-is-current-env} = \gad{AND}(\var{head-is-current-env0}, \var{head-is-a-sym})$.
- Let $\var{head-is-if} = \gad{AND}(\var{head-is-if0}, \var{head-is-a-sym})$.
- Let $\var{head-is-any} = \gad{OR}(\var{head-is-quote}, \var{head-is-if}, \var{head-is-lambda}, \var{head-is-current-env}, \var{head-is-let-or-letrec}, \var{head-is-unop},\var{head-is-binop})$.
- Let $\var{head-potentially-fun-type} = \gad{OR}(\var{head-is-a-sym}, \var{head-is-a-cons}, \var{head-is-fun})$.
- Let $\var{head-potentially-fun} = \gad{AND}(\var{head-potentially-fun-type}, \var{head-is-any}.\gad{not}())$.
- Let $\var{rest-is-nil} = \var{rest}.\gad{IS-NIL}()$.
- Let $\var{rest-is-cons} = \gad{IS-CONS}(\var{rest})$.
- Let $\var{expr-cdr-not-dummy} = \gad{AND}(\var{not-dummy}, \var{rest-is-nil}.\gad{NOT}(), \var{rest-is-cons}, \var{head-is-any}, \var{head-is-current-env}.\gad{NOT}())$.
- Let $\var{is-dotted-error} = \gad{AND}(\var{rest-is-nil}.\gad{NOT}(), \var{rest-is-cons}.\gad{NOT}(), \var{expr-cdr-not-dummy}.\gad{NOT}())$.
- Let $(\var{arg1}, \var{more}) = \gad{CAR-CDR-NAMED}(\var{rest}, \var{cons-names.expr-cdr}, \var{allocated-cons-witness}, \var{expr-cdr-not-dummy})$.
- Let $\var{more-is-nil} = \gad{ALLOC-EQUAL}(\var{more}, \var{globals.nil-ptr})$.
- Let $\var{is-binop-missing-arg-error} = \gad{AND}(\var{head-is-binop}, \var{more-is-nil}, \var{head-is-begin}.\gad{NOT}(), \var{head-is-eval}.\gad{NOT}())$.
- Let $\var{arg1-is-cons} = \gad{IS-CONS}(\var{arg1})$.
- Let $\var{arg1-is-str} = \gad{IS-STR}(\var{arg1})$.
- Let $\var{arg1-is-nil} = \var{arg1}.\gad{IS-NIL}()$.
- Let $\var{expr-cadr-not-dummy0} = \gad{OR}(\var{arg1-is-cons}, \var{arg1-is-nil}, \var{arg1-is-str})$.
- Let $\var{expr-cadr-not-dummy} = \gad{AND}(\var{expr-cdr-not-dummy}, \var{expr-cadr-not-dummy0}, \var{head-is-lambda})$.
- Let $(\var{car-args}, \var{cdr-args}) = \gad{CAR-CDR-NAMED}(\var{arg1}, \var{cons-names.expr-cadr}, \var{allocated-cons-witness}, \var{expr-cadr-not-dummy})$.
- Let $\var{end-is-nil} = \var{more}.\gad{IS-NIL}()$.
In many cases, we need to compute a new pointer, which requires the calculation of the hash function. Since this operation is expensive in the circuit, we want to avoid it as much as possible. In order to do that, we use a multicase gadget to select the preimage in those situations. Then we compute the hash only once. Later, a second multicase is used to select the final result.
- Let $\var{default-num-pair} = (\var{globals}.\var{default-num}, \var{globals}.\var{default-num})$.
$\rm{\small{\bold{Case}~head~\bold{is}~lambda}}$.
A lambda expression receives a list of arguments and a body expression as input. We use one-argument lambdas as building blocks. In order to deal with multiple arguments, we recursively use nested one-argument lambdas. If the list of arguments is empty, we use a dummy argument instead. Otherwise, we take the first argument to build the function and construct an inner body that itself is another lambda expression containing the rest of the list of arguments and the same body, and use that function to call apply-continuation.
- Let $(\var{args}, \var{body}) = (\var{arg1}, \var{more})$.
- Let $\var{args-is-nil} = \var{args}.\gad{IS-NIL}()$.
- Let $\var{cdr-args-is-nil} = \var{cdr-args}.\gad{IS-NIL}()$.
- Let $\var{arg} = \gad{PICK}(\var{args-is-nil}, \var{globals.dummy-arg-ptr}, \var{car-args})$.
- Let $\var{arg-is-sym} = \var{arg}.\gad{IS-SYM}()$.
- Let $\var{lambda-not-dummy} = \gad{AND}(\var{head-is-lambda}, \var{not-dummy}, \var{cdr-args-not-nil})$.
- Let $\var{inner-not-dummy} = \gad{AND}(\var{lambda-not-dummy}, \var{cdr-args-is-nil}.\gad{NOT}())$.
- Let $\var{inner} = \gad{CONSTRUCT-CONS-NAMED}(\var{cdr-args}, \var{body}, \var{cons-names.inner-lambda}, \var{allocated-cons-witness}, \var{inner-not-dummy}).$
- Let $l = \gad{CONSTRUCT-CONS-NAMED}(\var{globals.lambda-sym}, \var{inner}, \var{cons-names.lambda}, \var{allocated-cons-witness}, \var{inner-not-dummy})$.
- Let $\var{list} = \gad{CONSTRUCT-CONS-NAMED}(l, \var{globals.nil-ptr}, \var{cons-names.inner-body}, \var{allocated-cons-witness}, \var{inner-not-dummy})$.
- Let $\var{inner-body} = \gad{PICK}(\var{cdr-args-is-nil}, \var{body}, \var{list})$.
- Let $\var{function} = \gad{CONSTRUCT-FUN}(\var{arg}, \var{inner-body}, \var{env})$.
- Let $\var{lambda-arg-error} = \gad{AND}(\var{arg-is-sym}.\gad{NOT}(), \var{lambda-not-dummy})$.
- Let $\var{lambda-expr} = \gad{PICK}(\var{lambda-arg-error}, \var{expr}, \var{function})$.
- Let $\var{lambda-cont} = \gad{PICK}(\var{lambda-arg-error}, \var{globals.error-ptr-cont}, \var{cont})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.lambda}, \var{lambda-expr}, \var{lambda-env}, \var{lambda-cont}, \var{globals.true-num})$.
$\rm{\small{\bold{Case}~head~\bold{is}~quote}}$.
- Let $\var{arg1-or-expr} = \gad{PICK}(\var{end-is-nil}, \var{arg1}, \var{expr})$.
- Let $\var{the-cont} = \gad{PICK}(\var{end-is-nil}, \var{cont}, \var{globals.error-ptr-cont})$.
- $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.quote}, \var{arg1-or-expr}, \var{env}, \var{the-cont}, \var{globals.true-num})$.
$\rm{\small{\bold{Case}~head~\bold{is}~let~\bold{or}~letrec}}$.
Because both let and letrec share common subcircuits, we are going to factor them out in order to reduce the number of constraints.
Initially, we have:
- Let (bindings, body) = (arg1, more).
- Let $\var{let-letrec-not-dummy} = \gad{AND}(\var{not-dummy}, \var{head-is-let-or-letrec})$.
- Let $(\var{bindings}, \var{body}) = (\var{arg1}, \var{more})$.
- Let $(\var{body1}, \var{rest-body}) = \gad{CAR-CDR-NAMED}(\var{body}, \var{cons-names.expr-cddr}, \var{allocated-cons-witness}, \var{let-letrec-not-dummy})$.
- Let $\var{bindings-is-nil} = \var{binding}.\gad{IS-NIL}()$.
- Let $\var{bindings-is-cons} = \gad{ALLOC-EQUAL}(\var{bindings.tag}(), \var{globals.cons-tag})$.
- Let $\var{body-is-nil} = \var{body}.\gad{IS-NIL}()$.
- Let $\var{rest-body-is-nil} = \var{rest-body}.\gad{IS-NIL}()$.
A let or a letrec expression will receive a list of bindings to be added to the environment and a body expression to be evaluated. If the list of bindings is empty, we just return it together with the current environment and continuation. If not, we take the first element of the list, add it to the environment, and recursively use another let or letrec to evaluate the rest of the list.
- Let $(\var{binding1}, \var{rest-bindings}) = (\var{car-args}, \var{cdr-args})$.
- Let $\var{expr-caadr-not-dummy} = \gad{AND}(\var{rest-body-is-nil}, \gad{body-is-nil}.\gad{NOT}(), \var{bindings-is-cons}, \var{bindings-is-nil}.\gad{NOT}(), \var{let-letrec-not-dummy})$.
- Let $(\var{var-let-letrec}, \var{vals}) = \cir{CAR-CDR-NAMED}(\var{binding1}, \var{cons-names.expr-caadr}, \var{allocated-cons-witness}, \var{expr-caadr-not-dummy})$.
- Let $\var{var-let-letrec-is-sym} = \var{var-let-letrec}.\gad{IS-SYM}()$.
- Let $\var{var-let-letrec-is-nil} = \var{var-let-letrec}.\gad{IS-NIL}()$.
- Let $\var{var-let-letrec-is-list} = \gad{OR}(\var{var-let-letrec-is-sym}, \var{var-let-letrec-is-nil})$.
- Let $\var{expr-caaadr-not-dummy} = \gad{AND}(\var{expr-caadr-not-dummy}, \gad{var-let-letrec-is-list})$.
- let $(\var{val}, \var{end}) = \var{CAR-CDR-NAMED}(\var{vals}, \var{cons-names.expr-caaadr}, \var{allocated-cons-witness}, \var{expr-caadr-not-dummy})$.
- Let $\var{end-is-nil} = \var{end}.\gad{IS-NIL}()$.
- Let $\var{cond-error} = \gad{OR}(\var{rest-body-is-nil}.\gad{NOT}(), \var{end-is-nil}.\gad{NOT}(), \var{body-is-nil}, \var{var-let-letrec-is-list}.\gad{NOT}())$.
- Let $\var{rest-bindings-is-nil} = \var{rest-bindings}.\gad{IS-NIL}()$.
- Let $\var{expanded-inner-not-dummy0} = \gad{AND}(\var{rest-bindings-is-nil}.\gad{NOT}(), \var{end-is-nil})$.
- Let $\var{expanded-inner-not-dummy} = \gad{AND}(\var{expanded-inner-not-dummy0}, \var{let-letrec-not-dummy}, \var{body-is-nil}.\gad{NOT}(),\var{rest-body-is-nil})$.
- Let $\var{expanded0} = \gad{CONSTRUCT-CONS-NAMED}(\var{rest-bindings}, \var{body}, \var{cons-names.expanded-inner}, \var{allocated-cons-witness}, \var{expanded-inner-not-dummy})$.
- Let $\var{expanded1} = \gad{CONSTRUCT-CONS-NAMED}(\var{head}, \var{expanded0}, \var{cons-names.expanded}, \var{allocated-cons-witness}, \var{expanded-inner-not-dummy})$.
- Let $\var{expanded} = \gad{PICK}(\var{rest-bindings-is-nil}, \var{body1}, \var{expanded1})$.
- Let $\var{output-expr} = \gad{PICK}(\var{bindings-is-nil}, \var{body1}, \var{val})$.
- Let $\var{the-expr} = \gad{PICK}(\var{cond-error}, \var{expr}, \var{output-expr})$.
- Let $\var{expanded-let} = \var{expanded}$.
- Let $\var{expanded-letrec} = \var{expanded}$.
- Let $\var{let-continuation-components} = [\var{var-let-letrec}, \var{expanded-let}, \var{env}, \var{cont}]$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{let-sym.value}(), \var{globals.let-cont-tag}, \var{let-continuation-components})$.
- Let $\var{letrec-continuation-components} [\var{var-let-letrec}, \var{expanded-letrec}, \var{env}, \var{cont}]$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.letrec}, \var{globals.letrec-cont-tag}, \var{letrec-continuation-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~eval}}$.
- Let $\var{the-op} = \gad{PICK}(\var{end-is-nil}, \var{globals.unop-cont-tag}, \var{globals.binop-cont-tag})$.
- Let $\var{op1-or-op2} = \gad{PICK}(\var{end-is-nil}, \var{globals.op1-eval-tag}, \var{globals.op2-eval-tag})$.
- Let $\var{cont-or-env-tag} = \gad{PICK}(\var{end-is-nil}, \var{cont.tag}(), \var{env.tag}())$.
- Let $\var{cont-or-env-hash} = \gad{PICK}(\var{end-is-nil}, \var{cont.hash}(), \var{env.hash}())$.
- Let $\var{default-or-expr-tag} = \gad{PICK}(\var{end-is-nil}, \var{globals.default-num}, \var{more.tag}())$.
- Let $\var{default-or-expr-hash} = \gad{PICK}(\var{end-is-nil}, \var{globals.default-num}, \var{more.hash}())$.
- Let $\var{default-or-cont-tag} = \gad{PICK}(\var{end-is-nil}, \var{globals.default-num}, \var{cont.tag}())$.
- Let $\var{default-or-cont-hash} = \gad{PICK}(\var{end-is-nil}, \var{globals.default-num}, \var{cont.hash}())$.
- Let $\var{eval-continuation-components} = [[\var{op1-or-op2}, \var{globals.default-num}], [\var{env-or-cont-tag}, \var{env-or-cont-hash}], [\var{default-or-expr-tag}, \var{default-or-expr-hash}], [\var{default-or-cont-tag}, \var{default-or-cont-hash}]]$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.eval}, \var{the-op}, \var{eval-continuation-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~cons}}$.
- Let $\var{cons-cont-components} = ((\var{globals.op2-cons-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.cons}, \var{globals.binop-cont-tag}, \var{cons-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~strcons}}$.
- Let $\var{strcons-cont-components} = ((\var{globals.op2-strcons-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.strcons}, \var{globals.binop-cont-tag}, \var{strcons-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~hide}}$.
- Let $\var{hide-cont-components} = ((\var{globals.op2-hide-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.hide}, \var{globals.binop-cont-tag}, \var{hide-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~commit}}$.
- Let $\var{commit-cont-components} = ((\var{globals}.\var{op1-commit-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.commit}, \var{globals}.\var{unop-cont-tag}, \var{commit-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~open}}$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{constants.open}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~u64}}$.
- Let $\var{u64-cont-components} = ((\var{globals}.\var{op1-u64-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants}.\var{u64}, \var{globals}.\var{unop-cont-tag}, \var{char-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~char}}$.
- Let $\var{char-cont-components} = ((\var{globals}.\var{op1-char-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants}.\var{char}, \var{globals}.\var{unop-cont-tag}, \var{char-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~car}}$.
- Let $\var{car-cont-components} = ((\var{globals}.\var{op1-char-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants}.\var{car}, \var{globals}.\var{unop-cont-tag}, \var{car-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~cdr}}$.
- Let $\var{cdr-cont-components} = (\var{globals}.\var{op1-car-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants}.\var{cdr}, \var{globals}.\var{unop-cont-tag}, \var{cdr-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~comm}}$.
- Let $\var{comm-cont-components} = ((\var{globals}.\var{op1-comm-tag}, \var{globals}.\var{default-num}), (\var{cont}.\fun{tag}(), \var{cont}.\fun{hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.comm}, \var{globals}.\var{unop-cont-tag}, \var{comm-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~num}}$.
- Let $\var{num-cont-components} = ((\var{globals.op1-num-tag}, \var{globals.default-num}), (\var{cont.tag}(), \var{cont.hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.num}, \var{globals.unop-cont-tag}, \var{num-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~atom}}$.
- Let $\var{atom-cont-components} = ((\var{globals.op1-atom-tag}, \var{globals.default-num}), (\var{cont.tag}(), \var{cont.hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.atom}, \var{globals.unop-cont-tag}, \var{atom-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~emit}}$.
- Let $\var{emit-cont-components} = ((\var{globals.op1-emit-tag}, \var{globals.default-num}), (\var{cont.tag}(), \var{cont.hash}()), \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.emit}, \var{globals.unop-cont-tag}, \var{emit-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~begin}}$.
- Let $\var{begin-cont-components} = ((\var{globals.op2-begin-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.begin}, \var{globals.binop-cont-tag}, \var{begin-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~+}}$.
- Let $\var{sum-cont-components} = ((\var{globals.op2-sum-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.sum}, \var{globals.binop-cont-tag}, \var{sum-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~–}}$.
- Let $\var{diff-cont-components} = ((\var{globals.op2-diff-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.diff}, \var{globals.binop-cont-tag}, \var{diff-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~/}}$.
- Let $\var{quotient-cont-components} = ((\var{globals.op2-diff-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.div}, \var{globals.binop-cont-tag}, \var{quotient-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~*}}$.
- Let $\var{product-cont-components} = ((\var{globals.op2-prod-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.mul}, \var{globals.binop-cont-tag}, \var{product-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}=}}$.
- Let $\var{numequal-cont-components} = ((\var{globals.rel2-numequal-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{contants.numequal}, \var{globals.binop-cont-tag}, \var{numequal-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~eq}}$.
- Let $\var{equal-cont-components} = ((\var{globals.rel2-numequal-tag}, \var{globals.default-num}), \var{env}, \var{more}, \var{cont})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constant.equal}, \var{globals.binop-cont-tag}, \var{equal-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~if}}$.
- Let $\var{if-cont-components} = (\var{more}, \var{cont}, \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{constants.if}, \var{globals.if-cont-tag}, \var{if-cont-components})$.
$\rm{\small{\bold{Case}~head~\bold{is}~current{-}env}}$.
- Let $\var{current-env-cont} = \gad{PICK}(\var{rest-is-nil}, \var{globals.error-ptr-cont}, \var{cont})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.current-env}, \var{env}, \var{env}, \var{globals.current-env-cont}, \var{globals.true})$.
$\rm{\footnotesize{Compute~the~hash~preimage~components}}$:
- Let $\var{preimage-result} = \gad{MULTICASE}(\var{preimage-clauses})$.
- Let $\var{newer-cont} = \gad{CONSTRUCT-FROM-COMPONENTS}(\var{preimage-components-result})$.
- Let $\var{newer-cont-if-end-is-nil} = \gad{PICK}(\var{end-is-nil}, \var{newer-cont}, \var{globals.error-ptr-cont})$.
- Let $\var{newer-cont-if-end-not-nil} = \gad{PICK}(\var{end-is-nil}, \var{globals.error-ptr-cont}, \var{newer-cont})$.
$\rm{\small{\bold{Case}~head~\bold{is}~let~\bold{or}~letrec}}$.
- Let $\var{output-cont} = \gad{PICK}(\var{bindings-is-nil}, \var{cont}, \var{newer-cont})$.
- Let $\var{the-cont-let-letrec} = \gad{PICK}(\var{cond-error}, \var{globals.error-ptr-cont}, \var{output-cont})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.let}, \var{the-expr}, \var{env}, \var{the-cont-let-letrec}, \var{globals.false})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.letrec}, \var{the-expr}, \var{env}, \var{the-cont-let-letrec}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~cons}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.cons}, \var{arg1}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~hide}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{contants.hide}, \var{arg1}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~begin}}$.
- Let $\var{the-cont-begin} = \gad{PICK}(\var{end-is-nil}, \var{cont}, \var{newer-cont})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{contants.begin}, \var{arg1}, \var{env}, \var{the-cont-begin}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~car}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{contants.car}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~cdr}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{contants.cdr}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~commit}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.commit}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~secret}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.secret}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~num}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.num}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~comm}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.comm}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~char}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.char}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~atom}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.atom}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~emit}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.emit}, \var{arg1-or-expr}, \var{env}, \var{newer-cont-if-end-not-nil}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~+}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.sum}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~–}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.diff}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~*}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.mul}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~/}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.div}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}=}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.numequal}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~eq}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.equal}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~if}}$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{constants.if-sym}, \var{arg1}, \var{env}, \var{newer-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~head~\bold{is}~(FN.ARGs)}}$.
- Let $\var{fun-form} = \var{head}$.
- Let $\var{more-args-is-nil} = \var{more}.\gad{IS-NIL}()$.
- Let $\var{args-is-nil-or-more-is-nil} = \gad{OR}(\var{rest-is-nil}, \var{more-args-is-nil})$.
- Let $\var{fn-not-dummy} = \gad{AND}(\var{args-is-nil-or-more-is-nil}.\gad{NOT}(), \var{head-is-any}.\gad{NOT}(), \var{not-dummy})$.
- Let $\var{expanded-inner0} = \gad{CONSTRUCT-CONS-NAMED}(\var{arg1}, \var{globals.nil-ptr}, \var{cons-names.expanded-inner0}, \var{allocated-cons-witness}, \var{fn-not-dummy})$.
- Let $\var{expanded-inner} = \gad{CONSTRUCT-CONS-NAMED}(\var{fun-form}, \var{expanded-inner0}, \var{cons-names.expanded-inner}, \var{allocated-cons-witness}, \var{fn-not-dummy})$.
- Let $\var{expanded} = \gad{CONSTRUCT-CONS-NAMED}(\var{expanded-inner}, \var{more}, \var{cons-names.fun-expanded}, \var{allocated-cons-witness}, \var{fn-not-dummy})$.
- Let $\var{res} = \var{PICK}(\var{args-is-nil-or-more-is-nil}, \var{fun-form}, \var{expanded})$.
- Let $\var{continuation} = \gad{PICK}(\var{args-is-nil-or-more-is-nil}, \var{newer-cont}, \var{cont})$.
- Let $\var{defaults} = [\var{res.tag}(), \var{res.hash}(), \var{env.tag}(), \var{env.hash}(), \var{continuation.tag}(), \var{continuation.hash}(), \var{globals.false-num}]$.
Finally, we compute the last multicase and return the result.
- Let $\var{results} = \gad{multi-case}(\var{head.hash}(), \var{clauses}, \var{defaults})$.
- Let $\var{result-expr} = \var{results}[0]$.
- Let $\var{result-env} = \var{results}[1]$.
- Let $\var{result-cont} = \var{results}[2]$.
- Let $\var{result-apply-cont} = \var{results}[3]$.
- Return $(\var{result-expr}, \var{result-env}, \var{result-cont}, \var{result-apply-cont})$.
Apply continuation #
$ \cirtitle{Circuit~3.4}~\cir{Apply-Continuation} \\ $
- $\cirio{INPUT} \var{result}, \var{env}, \var{cont}, \var{witness}$.
- $\cirio{OUTPUT} \var{expr}, \var{env}, \var{cont}$.
- $\com{Do pre-pointer computations, adding clauses to both multicases}$.
- $\var{preimage} = \gad{MULTICASE}(\var{preimage-clauses})$.
- $\com{Calculate newer continuation pointer}$.
- $\com{Do post-pointer computations, adding clauses to second multicase}$.
- $\var{result} = \gad{MULTICASE}(\var{clauses})$.
- Return $\var{result}$.
Initially, we do:
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{cont-tags.outermost}, \var{result}, \var{env}, \var{globals.terminal-ptr}, \var{globals.false-num}, \var{globals.false-num})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{cont-tags.terminal}, \var{result}, \var{env}, \var{globals.terminal-ptr}, \var{globals.false-num}, \var{globals.false-num})$.
- Call $\var{clauses}.\gad{ADD-CLAUSE}(\var{cont-tags.error}, \var{result}, \var{env}, \var{globals.error-cont-ptr}, \var{globals.false-num}, \var{globals.false-num})$.
- Let $\var{cont-is-terminal} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.terminal-tag}())$.
- Let $\var{cont-is-dummy} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.dummy-tag}())$.
- Let $\var{cont-is-error} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.error-tag}())$.
- Let $\var{cont-is-outermost} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.outermost-tag}())$.
- Let $\var{cont-is-trivial} = \gad{OR}(\var{cont-is-terminal}, \var{cont-is-dummy}, \var{cont-is-error}, \var{cont-is-outermost})$.
- Let $\var{apply-continuation-components-not-dummy} = \gad{AND}(\var{cont-is-trivial}.\gad{NOT}(), \var{not-dummy})$.
- Let $(\var{continuation-tag}, \var{continuation-components}) = \fun{get-named-components}(\var{cont}, \var{cons-names.apply-continuation}, \var{allocated-cont-witness}, \var{apply-continuation-components-not-dummy})$.
- Let $\var{continuation} = \var{continuation-components}[0]$.
- call $\var{clauses}.\gad{ADD-CLAUSE}(\var{cont-tag.emit}, \var{result}, \var{env}, \var{continuation}, \var{globals.true-num}, \var{globals.false-num})$.
- Let $\var{preimage-clauses} = \gad{MULTICASE-CLAUSES}()$.
- Let $\var{cont-components} = \fun{get-cont-components}(\var{witness})$.
- Let $\var{default-num-pair} = (\var{globals.default-num},\var{globals.default-num})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call0}}$.
- Let $\var{old-components} = (\var{cont-components}[0], \var{cont-components}[1], \var{cont-components}[2], \var{cont-components}[3])$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.call0-sym}, \var{globals.tail-cont-tag}, \var{old-cont-components})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call}}$.
- Let $\var{call-components} = (\var{cont-components}[0], \var{result}, \var{cont-components}[2], \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.call-sym}, \var{globals.call2-cont-tag}, \var{call-components})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call2}}$.
- Let $\var{all2-components} = (\var{saved-env}, \var{continuation}, \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.call2-sym}, \var{globals.tail-cont-tag}, \var{call2-components})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~let}}$.
- Let $\var{let-components} = (\var{cont-components}[2], \var{cont-components}[3], \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.let-sym}, \var{globals.tail-cont-tag}, \var{let-components})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~letrec}}$.
- Let $\var{letrec-components} = (\var{cont-components}[2], \var{cont-components}[3], \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.letrec-sym}, \var{globals.tail-cont-tag}, \var{letrec-components})$.
At this point we need to add commitment constraints that are going to be useful later.
- Let $\var{operator} = \var{continuation-components}[0]$.
- Let $\var{is-op2-hide} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op2-hide-tag}, \var{operator.tag}())$.
- Let $\var{is-op1-open} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-open-tag}, \var{operator.tag}())$.
- Let $\var{is-op1-secret} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-secret-tag}, \var{operator.tag}())$.
- Let $\var{is-op1-open-or-secret} = \gad{OR}(\var{is-op1-open}, \var{is-op1-secret})$.
- Let $\var{digest} = \var{result.hash}()$.
- Let $(\var{secret-res}, \var{open-res}) = \gad{NON-DETERMINISTIC-OPEN-SECRET}(\var{expr-tag.comm}, \var{digest})$.
- Let $\var{open-expr} = \gad{ALLOC}(\var{open-res})$.
- Let $\var{open-secret} = \gad{ALLOC}(\var{secret-res})$.
- Let $\var{arg1} = \var{continuation-components}[1]$.
- Let $\var{commit-secret} = \gad{PICK}(\var{is-op2-hide}, \var{arg1.hash}(), \var{globals.default-num})$,
- Let $\var{secret} = \gad{PICK}(\var{is-op1-open-or-secret}, \var{open-secret}, \var{commit-secret})$.
- Let $\var{committed} = \gad{PICK}(\var{is-op1-open}, \var{open-expr}, \var{result})$.
- Let $\var{commitment} = \gad{HIDE}(\var{secret}, \var{committed})$.
- Let $\var{commitment-secret} = \var{secret}$.
- Let $\var{committed-expr} = \var{committed}$.
let (unop_val, unop_continuation) = {
$\rm{\small{\bold{Case}~ cont~\bold{is}~unop}}$.
- Let $\var{op1} = \var{continuation-components}[0]$.
- Let $\var{unop-continuation} = \var{continuation-components}[1]$.
- Let $\var{cont-is-unop} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.unop-cont-tag})$.
- Let $\var{unop-op-is-car} = \gad{ALLOC-TAG-EQUAL}(\var{op1.tag}(), \var{globals.op1-car-tag})$.
- Let $\var{unop-op-is-cdr} = \gad{ALLOC-TAG-EQUAL}(\var{op1.tag}(), \var{globals.op1-cdr-tag})$.
- Let $\var{unop-op-is-car-or-cdr} = \gad{OR}(\var{unop-op-is-car}, \var{unop-op-is-cdr})$.
- Let $\var{result-is-cons} = \gad{ALLOC-TAG-EQUAL}(\var{result.tag}(), \var{globals.cons-tag})$.
- Let $\var{result-is-str} = \gad{ALLOC-TAG-EQUAL}(\var{result.tag}(), \var{globals.str-tag})$.
- Let $\var{result-is-empty-str} = \gad{ALLOC-EQUAL}(\var{result}, \var{globals.empty-str-ptr})$.
- Let $\var{result-is-cons-like} = \gad{OR}(\var{result-is-cons}, \var{result-is-str})$.
- Let $\var{unop-cons-not-dummy} = \gad{AND}(\var{cont-is-unop}, \var{unop-op-is-car-or-cdr}, \var{result-is-cons-like}, \var{result-is-empty-str}.\gad{NOT}())$.
- Let $(\var{allocated-car}, \var{allocated-cdr}) = \gad{CAR-CDR-NAMED}(\var{result}, \var{cons-names.unop-cons-like}, \var{allocated-cons-witness}, \var{unop-cons-not-dummy})$.
- Let $\var{res-car} = \gad{PICK}(\var{result-is-empty-str}, \var{globals.nil-ptr}, \var{allocated-car})$.
- Let $\var{res-cdr} = \gad{PICK}(\var{result-is-empty-str}, \var{globals.empty-str-ptr}, \var{allocated-cdr})$.
- Let $\var{is-atom-ptr} = \gad{PICK}(\var{result-is-cons}, \var{globals.nil-ptr}, \var{globals.t-ptr})$.
- Let $\var{num} = \gad{TO-NUM}(\var{result})$.
- Let $\var{comm} = \gad{TO-COMM}(\var{result})$.
- Let $(\var{u32-elem}, \var{u64-elem}) = \gad{to-unsigned-integers}(\var{result.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.car-tag}, (\var{res-car.tag}(), \var{res-car.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.cdr-tag}, (\var{res-cdr.tag}(), \var{res-cdr.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.atom-tag}, (\var{is-atom-ptr.tag}(), \var{is-atom-ptr.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.emit-tag}, (\var{result.tag}(), \var{result.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.commit-tag}, (\var{commitment.tag}(), \var{commitment.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.open-tag}, (\var{committed-expr.tag}(), \var{commitment.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.secret-tag}, (\var{globals.num-tag}, \var{commitment-secret}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.num-tag}, (\var{globals.num-tag}, \var{num.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.u64-tag}, (\var{globals.u64-tag}, \var{u64-elem}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.comm-tag}, (\var{comm.tag}(), \var{comm.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.char-tag}, (\var{globals.char-tag}, \var{is-atom-ptr.hash}())$.
- Call $\var{unop-clauses}.\gad{ADD-CLAUSE}(\var{op1.eval-tag}, (\var{result.tag}(), \var{result.hash}())$.
- Let $\var{res} = \gad{MULTI-CASE}(\var{op1.tag}(), \var{unop-clauses})$.
- let $\var{unop-val} = \var{res}[0]$.
- Let $\var{emit-components} = (\var{unop-continuation}, \var{default-num-pair}, \var{default-num-pair}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.unop-tag}, \var{globals.emit-cont-tag}, \var{emit-components})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~binop}}$.
- Let $\var{unop-continuation} = \var{cont-components}[3]$.
- Let $\var{binop-components} = (\var{cont-components}[0], \var{result}, \var{unop-continaution}, \var{default-num-pair})$.
- Call $\var{preimage-clauses}.\gad{ADD-CLAUSE}(\var{globals.binop-tag}, \var{globals.binop2-cont-tag}, \var{binop-components})$.
$\rm{\footnotesize{Compute~the~hash~preimage~components}}$:
- Let $\var{preimage-result} = \gad{MULTICASE}(\var{preimage-clauses})$.
- Let $\var{newer-cont} = \gad{CONSTRUCT-FROM-COMPONENTS}(\var{preimage-result})$.
We define $\var{result-is-fun}$, which is used in Call0, Call and Call2, as follows:
- Let $\var{result-is-fun} = \gad{IS-FUN}(\var{function})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call0}}$.
- Let $\var{continuation} = \var{continuation-components}[1]$.
- Let $\var{cont-is-call0} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.call0-cont-tag})$.
- Let $\var{call0-not-dummy} = \gad{AND}(\var{cont-is-call0}, \var{result-is-fun}, \var{not-dummy})$.
- Let $(\var{fun-hash}, \var{arg-t}, \var{body-t}, \var{closed-env}) = \gad{ALLOCATE-MAYBE-FUN-UNCONSTRAINED}(\var{result})$.
- Call $\gad{IMPLIES-EQUAL}(\var{call0-not-dummy}, \var{fun-hash}, \var{result.hash}())$.
- Let $\var{args-is-dummy} = \gad{alloc-equal}(\var{arg-t}, \var{gobals.dummy-arg-ptr})$.
- Let $\var{body-t-is-cons} = \gad{ALLOC-EQUAL}(\var{body-t.tag}(), \var{globals.cons-tag})$.
- Let $\var{body-t-is-nil} = \var{body-t}.\gad{IS-NIL}()$.
- Let $\var{body-t-is-list} = \gad{OR}(\var{body-t-is-cons}, \var{body-t-is-list})$.
- Let $\var{zero-arg-call-not-dummy} = \gad{AND}(\var{call0-not-dummy}, \var{body-t-is-list}, \var{args-is-dummy})$.
- Let $(\var{body-form}, \var{end}) = \gad{CAR-CDR-NAMED}(\var{body-t}, \var{cons-names.fun-body}, \var{allocated-cons-witness}, \var{zero-arg-call-not-dummy})$.
- Let $\var{end-is-nil} = \var{end}.\gad{IS-NIL}()$.
- Let $\var{continuation-is-tail} = \gad{ALLOC-TAG-EQUAL}(\var{continuation.tag}(), \var{globals.tail-cont-tag})$.
- Let $\var{tail-cont} = \gad{PICK}(\var{continuation-is-tail}, \var{continuation}, \var{newer-cont2})$.
- Let $\var{next-expr} = \gad{PICK}(\var{args-is-dummy}, \var{body-form}, \var{result})$.
- Let $\var{next-env} = \gad{PICK}(\var{args-is-dummy}, \var{closed-env}, \var{env})$.
- Let $\var{next-cont} = \gad{PICK}(\var{args-is-dummy}, \var{tail-cont}, \var{continuation})$.
- Let $\var{body-form-is-nil} = \var{body-form}.\gad{IS-NIL}()$.
- Let $\var{body-is-well-formed} = \gad{AND}(\var{body-form-is-nil}.\gad{NOT}(), \var{end-is-nil})$.
- Let $\var{result-is-valid-fun} = \gad{AND}(\var{result-is-fun}, \var{body-is-well-formed})$.
- Let $\var{result-is-valid-zero-arg-fun} = \gad{AND}(\var{result-is-valid-fun}, \var{arg-is-dummy})$.
- Let $\var{the-expr} = \gad{PICK}(\var{result-is-valid-zero-arg-fun}, \var{next-expr}, \var{result})$.
- Let $\var{the-env} = \gad{PICK}(\var{result-is-fun}, \var{next-env}, \var{env})$.
- Let $\var{result-not-fun-and-zero-arg-call-is-dummy} = \gad{AND}(\var{zero-arg-call-not-dummy}.\gad{NOT}(), \var{result-is-fun})$.
- Let $\var{the-cont-not-error} = \gad{OR}(\var{result-is-valid-fun}, \var{result-not-fun-and-zero-arg-call-is-dummy})$.
- Let $\var{the-cont} = \gad{PICK}(\var{the-cont-not-error}, \var{next-cont}, \var{globals.error-ptr-cont})$.
- Let $\var{newer-cont2-not-dummy0} = \gad{AND}(\var{continuation-is-tail}.\gad{NOT}(), \var{args-is-dummy}, \var{result-is-fun})$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{newer-cont2-not-dummy0})$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{cont-tag.call0}, \var{the-expr}, \var{the-env}, \var{the-cont}, \var{globals.false-num}, \var{newer-cont2-not-dummy})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call}}$.
- Let $\var{next-expr} = \var{continuation-components}[1]$.
- Let $\var{next-expr} = \gad{PICK}(\var{result-is-fun}, \var{next-expr}, \var{result})$.
- Let $\var{the-cont} = \gad{PICK}(\var{result-is-fun}, \var{newer-cont2}, \var{globals.error-ptr-cont})$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{cont-tag.call}, \var{next-expr}, \var{env}, \var{the-cont}, \var{globals.false-num}, \var{newer-cont2-not-dummy})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~call2}}$.
- Let $\var{fun} = \var{cont-components}[1]$.
- Let $\var{continuation} = \var{cont-components}[2]$.
- Let $\var{cont-is-call2-precomp} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.call2-cont-tag})$.
- Let $\var{cont-is-call2-and-not-dummy} = \gad{AND}(\var{cont-is-call2-precomp}, \var{not-dummy})$.
- Let $(\var{hash}, \var{arg-t}, \var{body-t}, \var{closed-env}) = \gad{ALLOCATE-MAYBE-FUN-UNCONSTRAINED}(\var{fun})$.
- Call $\gad{IMPLIES-EQUAL}(\var{cont-is-call2-and-not-dummy}, \var{fun.hash}(), \var{hash})$.
- Let $\var{args-is-dummy} = \gad{ALLOC-EQUAL}(\var{arg-t}, \var{globals.dummy-arg-ptr})$.
- Let $\var{args-is-not-dummy} = \var{args-is-dummy}.\gad{NOT}()$.
- Let $\var{cont-is-call2-and-not-dummy-and-not-dummy-args} = \gad{AND}(\var{cont-is-call2-and-not-dummy}, \var{args-is-not-dummy})$.
- Let $(\var{body-form}, \var{end}) = \gad{CAR-CDR-NAMED}(\var{body-t}, \var{cons-names.fun-body}, \var{allocated-cons-witness}, \var{cont-is-call2-and-not-dummy-and-not-dummy-args})$.
- Let $\var{body-form-is-nil} = \var{body-form}.\gad{IS-NIL}()$.
- Let $\var{end-is-nil} = \var{end}.\gad{IS-NIL}()$.
- Let $\var{body-is-well-formed} = \gad{AND}(\var{body-form-is-nil}.\gad{NOT}(), \var{end-is-nil})$.
- Let $\var{extend-not-dummy} = \gad{AND}(\var{cont-is-call2-and-not-dummy}, \var{args-is-dummy}.\gad{NOT}(), \var{body-is-well-formed})$.
- Let $\var{newer-env} = \gad{Extend-named}(\var{closed-env}, \var{arg-t}, \var{result}, \var{cons-names.closed-env}, \var{allocated-cons-witness}, \var{extend-not-dummy})$.
- Let $\var{continuation-is-tail} = \gad{ALLOC-TAG-EQUAL}(\var{continuation.tag}(), \var{globals.tail-cont-tag})$.
- Let $\var{tail-cont} = \gad{PICK}(\var{continuation-is-tail}, \var{continuation}, \var{newer-cont2})$.
- Let $\var{cond0} = \gad{OR}(\var{args-is-dummy}.\gad{not}(), \var{result-is-fun})$.
- Let $\var{cond} = \gad{AND}(\var{cond0}, \var{body-is-well-formed})$.
- Let $\var{the-cont} = \gad{PICK}(\var{cond}, \var{tail-cont}, \var{globals.error-ptr-cont})$.
- Let $\var{the-env} = \gad{PICK}(\var{cond}, \var{newer-env}, \var{env})$.
- Let $\var{the-expr} = \gad{PICK}(\var{cond}, \var{body-form}, \var{result})$.
- Let $\var{newer-cont2-not-dummy0} = \gad{AND}(\var{continuation-is-tail}.\gad{NOT}(), \var{cond})$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{newer-cont2-not-dummy0})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~binop}}$.
- Let $\var{operator} = \var{continuation-components}[0]$.
- Let $\var{saved-env} = \var{continuation-components}[1]$.
- Let $\var{unevaled-args} = \var{continuation-components}[2]$.
- Let $\var{cont-is-binop} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.binop-cont-tag})$.
- Let $\var{binop-not-dummy} = \gad{AND}(\var{cont-is-binop}, \var{not-dummy})$.
- Let $(\var{allocated-arg2}, \var{allocated-rest}) = \gad{CAR-CDR-NAMED}(\var{unevaled-args}, \var{cons-names.unevaled-args}, \var{allocated-cons-witness}, \var{binop-not-dummy})$.
- Let $\var{op-is-begin} = \gad{ALLOC-TAG-EQUAL}(\var{operator.tag}(), \var{globals.op2-begin-tag})$.
- Let $\var{rest-is-nil} = \gad{ALLOC-EQUAL}(\var{allocated-rest}, \var{globals.nil-ptr})$.
- Let $\var{rest-not-nil} = \var{rest-is-nil}.\gad{NOT}()$.
- Let $\var{begin} = \gad{GET-BEGIN}()$.
- Let $\var{allocated-begin} = \gad{ALLOC-PTR}(\var{begin})$.
- Let $\var{begin-not-dummy} = \gad{AND}(\var{op-is-begin}, \var{binop-not-dummy}, \var{rest-not-nil})$.
- Let $\var{begin-again} = \gad{CONSTRUCT-CONS-NAMED}(\var{allocated-begin}, \var{unevaled-args}, \var{cons-name.begin}, \var{allocated-cons-witness}, \var{begin-not-dummy})$.
- Let $\var{the-expr-if-begin} = \gad{PICK}(\var{op-is-begin}, \var{begin-again}, \var{result})$.
- Let $\var{otherwise} = \var{op-is-begin}.\gad{NOT}()$.
- Let $\var{otherwise-and-rest-is-nil} = \gad{AND}(\var{otherwise}, \var{rest-is-nil})$.
- Let $\var{the-expr} = \gad{PICK}(\var{rest-is-nil}, \var{allocated-arg2}, \var{the-expr-if-begin})$.
- Let $\var{the-env} = \gad{PICK}(\var{rest-is-nil}, \var{saved-env}, \var{env})$.
- Let $\var{the-cont-otherwise} = \gad{PICK}(\var{otherwise-and-rest-is-nil}, \var{newer-cont2}, \var{globals.error-ptr-cont})$.
- Let $\var{the-cont} = \gad{PICK}(\var{otherwise}, \var{the-cont-otherwise}, \var{continuation})$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{otherwise-and-rest-is-nil})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~binop2}}$.
- Let $\var{op2} = \var{cont-components}[0]$.
- Let $\var{arg1} = \var{cont-components}[1]$.
- Let $\var{continuation} = \var{cont-components}[2]$.
- Let $\var{arg2} = \var{result}$.
- Let $\var{arg1-is-num} = \gad{IS-NUM}(\var{arg1})$.
- Let $\var{arg2-is-num} = \gad{IS-NUM}(\var{arg2})$.
- Let $\var{both-args-are-num} = \gad{AND}(\var{arg1-is-num}, \var{arg2-is-num})$.
- Let $\var{arg1-is-u64} = \gad{IS-U64}(\var{arg1})$.
- Let $\var{arg2-is-u64} = \gad{IS-U64}(\var{arg2})$.
- Let $\var{both-args-are-u64s} = \gad{and}(\var{arg1-is-u64}, \var{arg2-is-u64})$.
- Let $\var{arg1-is-num-and-arg2-is-u64} = \gad{AND}(\var{arg1-is-num}, \var{arg2-is-u64})$.
- Let $\var{arg1-is-u64-and-arg2-is-num} = \gad{AND}(\var{arg1-is-u64}, \var{arg2-is-num})$.
- Let $\var{args-are-num-or-u64} = \gad{OR}(\var{both-args-are-nums}, \var{both-args-are-u64s}, \var{arg1-is-num-and-arg2-is-u64}, \var{arg1-is-u64-and-arg2-is-num})$.
- Let $\var{arg1-u64-to-num} = \gad{TO-NUM}(\var{arg1})$.
- Let $\var{arg1-final} = \gad{PICK}(\var{arg1-is-u64-and-arg2-is-num}, \var{arg1-u64-to-num}, \var{arg1})$.
- Let $\var{arg2-u64-to-num} = \gad{TO-NUM}(\var{arg2})$.
- Let $\var{arg2-final} = \gad{PICK}(\var{arg1-is-num-and-arg2-is-u64}, \var{arg2-u64-to-num}, \var{arg2})$.
- Let $a = \var{arg1.hash}()$.
- Let $b = \var{arg2.hash}()$.
- Let $\var{args-equal} = \gad{AND}(\var{arg1-final}, \var{arg2-final})$.
- Let $\var{args-equal-ptr} = \gad{PICK}(\var{args-equal}, \var{globals.t-ptr}, \var{globals.nil-ptr})$.
- Let $\var{not-dummy} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.binop2-cont-tag})$.
- Let $\var{sum} = \gad{ADD}(a, b)$.
- Let $\var{diff} = \gad{SUB}(a, b)$.
- Let $\var{product} = \gad{MUL}(a, b)$.
- Let $\var{op2-is-div} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-quotient-tag})$.
- Let $\var{op2-is-mod} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-modulo-tag})$.
- Let $\var{op2-is-div-or-mod} = \gad{OR}(\var{op2-is-div}, \var{op2-is-mod})$.
- Let $\var{b-is-zero} = \gad{ALLOC-IS-ZERO}(b)$.
- Let $\var{divisor} = \gad{PICK}(\var{b-is-zero}, 1, b)$ - if b is zero, take a dummy divisor.
- Let $\var{quotient} = \gad{DIV}(a, b)$.
- Let $\var{is-cons} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-cons-tag})$.
- Let $\var{is-strcons} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-strcons-tag})$.
- Let $\var{is-cons-or-strcons} = \gad{OR}(\var{is-cons}, \var{is-strcons})$.
- Let $\var{arg1-is-char} = \gad{ALLOC-TAG-EQUAL}(\var{arg1.tag}(), \var{globals.char-tag})$.
- Let $\var{arg2-is-str} = \gad{ALLOC-TAG-EQUAL}(\var{arg2.tag}(), \var{globals.str-tag})$.
- Let $\var{args-are-char-str} = \gad{AND}(\var{arg1-is-char}, \var{arg2-is-str})$.
- Let $\var{args-not-char-str} = \var{args-are-char-str}.\gad{NOT}()$.
- Let $\var{invalid-strcons-tag} = \gad{AND}(\var{args-not-char-str}, \var{is-strcons})$.
- Let $\var{cons-not-dummy} = \gad{AND}(\var{is-cons-or-strcons}, \var{not-dummy}, \var{invalid-strcons-tag}.\gad{NOT}())$.
- Let $\var{cons} = \gad{CONSTRUCT-CONS-NAMED}(\var{arg1}, \var{arg2}, \var{cons-names.the-cons}, \var{allocated-cons-witness}, \var{cons-not-dummy})$.
- Let $\var{op2-clauses} = \gad{CASE-CLAUSES}()$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.sum-tag}, \var{sum})$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.diff-tag}, \var{diff})$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.product-tag}, \var{product})$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{quotient-tag}, \var{quotient})$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.equal-tag}, \var{args-equal-ptr.hash}())$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.numequal-tag}, \var{args-equal-ptr.hash}())$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.cons-tag}, \var{cons.hash}())$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{globals.strcons-tag}, \var{cons.hash}())$.
- Call $\var{op2-clauses}.\gad{ADD-CLAUSE}(\var{hide-tag}, \var{commitment.hash}())$.
- Let $\var{default} = \var{globals.default-num}$.
- Let $\var{val} = \gad{CASE}(\var{op2.tag}(), \var{op2-clauses}, \var{default})$.
- Let $\var{is-equal} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-equal-tag})$.
- Let $\var{is-num-equal} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-num-equal-tag})$.
- Let $\var{is-equal–or-num-equal} = \gad{OR}(\var{is-equal}, \var{is-num-equal})$.
- Let $\var{op2-is-hide} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-hide-tag})$.
- Let $\var{commitment-tag-is-comm} = \gad{IS-COMM}(\var{commitment})$.
- Let $\var{commitment-tag-is-dummy} = \gad{ALLOC-IS-ZERO}(\var{commitment.tag}())$.
- Let $\var{commitment-tag-is-correct} = \gad{OR}(\var{commitment-tag-is-comm}, \var{commitment-tag-is-dummy})$.
- call $\gad{ENFORCE-IMPLICATION}(\var{op2-is-hide}, \var{commitment-tag-is-correct})$.
- Let $\var{cons-tag} = \gad{PICK}(\var{is-strcons}, \var{globals.str-tag}, \var{globals.cons-tag})$.
- Let $\var{comm-or-num-tag} = \gad{PICK}(\var{op2-is-hide}, \var{globals.comm-tag}, \var{globals.num-tag})$.
- Let $\var{is-cons-or-hide} = \gad{OR}(\var{is-cons}, \var{op2-is-hide})$.
- Let $\var{is-cons-or-strcons-or-hide-or-equal} = \gad{OR}(\var{is-cons-or-hide}, \var{is-strcons}, \var{is-equal})$.
- Let $\var{is-cons-or-strcons-or-hide-or-equal-or-num-equal} = \gad{OR}(\var{is-cons-or-strcons-or-hide-or-equal}, \var{is-num-equal})$.
- Let $\var{res-tag0} = \gad{PICK}(\var{is-cons-or-strcons}, \var{cons-tag}, \var{comm-or-num-tag})$.
- Let $\var{res-tag} = \gad{PICK}(\var{is-equal-or-num-equal}, \var{args-equal-ptr.tag}(), \var{res-tag0})$.
- Let $\var{res} = \gad{ALLOC-FROM-PARTS}(\var{res-tag}, \var{val})$.
- Let $(\var{is-comparison-tag}, \var{comp-val}, \var{diff-is-negative}) = \cir{COMPARISON-HELPER}(a, b, \var{diff}, \var{p2.tag}())$.
- Let $\var{field-arithmetic-result} = \gad{PICK}(\var{is-comparison-tag}, \var{comp-val}, \var{res})$.
- Let $\var{field-arithmetic-result-plus-2p64} = \gad{ADD}(\var{field-arithmetic-result.hash}(), \var{globals.power2-64-num})$.
- Let $\var{op2-is-diff} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-diff-tag})$.
- Let $\var{diff-is-negative-and-op2-is-diff} = \gad{AND}(\var{diff-is-negative}, \var{op2-is-diff})$.
- Let $\var{field-arith-and-u64-diff-result} = \gad{PICK}(\var{diff-is-negative-and-op2-is-diff}, \var{field-arithmetic-result-plus-2p64}, \var{field-arithmetic-result.hash}())$.
- Let $\var{coerce-to-u64} = \gad{TO-U64}(\var{field-arith-and-u64-diff-result})$.
- Let $\var{coerce-to-u64-ptr} = \gad{from-parts}(\var{globals.u64-tag}, \var{coerce-to-u64})$.
- Let $\var{both-args-are-u64s-and-not-comparison} = \gad{AND}(\var{both-args-are-u64s}, \var{is-comparison-tag}.\gad{NOT}())$.
- Let $\var{partial-u64-result} = \gad{PICK}(\var{both-args-are-u64s-and-not-comparison}, \var{coerce-to-u64-ptr}, \var{field-arithmetic-result})$.
- Let $(\var{alloc-q}, \var{alloc-r}) = \gad{ENFORCE-U64-DIV-MOD}(\var{op2-is-mod}, \var{arg1}, \var{arg2})$.
- Let $\var{alloc-q-ptr} = \gad{from-parts}(\var{globals.u64-tag}, \var{alloc-q})$.
- Let $\var{alloc-r-ptr} = \gad{from-parts}(\var{globals.u64-tag}, \var{alloc-r})$.
- Let $\var{op2-is-div-and-args-are-u64s} = \gad{AND}(\var{op2-is-div}, \var{both-args-are-u64s})$.
- Let $\var{include-u64-quotient} = \gad{PICK}(\var{op2-is-div-and-args-are-u64s}, \var{alloc-q-ptr}, \var{partial-u64-result})$.
- Let $\var{op2-is-mod-and-args-are-u64s} = \gad{AND}(\var{op2-is-mod}, \var{both-args-are-u64s})$.
- Let $\var{op2-is-mod-and-args-are-not-u64s} = \gad{AND}(\var{op2-is-mod}, \var{both-args-are-u64s}.\gad{NOT}())$.
- Let $\var{arithmetic-result} = \gad{PICK}(\var{op2-is-mod-and-args-are-u64s}, \var{alloc-r-ptr}, \var{include-u64-quotient})$.
- Let $\var{valid-types} = \gad{OR}(\var{is-cons-or-strcons-or-hide-or-equal}, \var{args-are-num-or-u64})$.
- Let $\var{real-div-or-more-and-b-is-zero} = \gad{AND}(\var{not-dummy}, \var{op2-is-div-or-mod}, \var{b-is-zero})$.
- Let $\var{valid-types-and-not-div-by-zero} = \gad{AND}(\var{valid-types}, \var{real-div-or-more-and-b-is-zero}.\gad{NOT}())$.
- Let $\var{op2-not-num-or-u64-and-not-cons-or-strcons-or-hide-or-equal-or-num-equal} = \gad{AND}(\var{args-are-num-or-u64}.\gad{NOT}(), \var{is-cons-or-strcons-or-hide-or-equal-or-num-equal}.\gad{NOT}())$.
- Let $\var{invalid-secret-tag-hide} = \gad{AND}(\var{arg1-is-u64}, \var{op2-is-hide})$.
- Let $\var{op2-is-hide-and-arg1-is-not-num} = \gad{AND}(\var{op2-is-hide}, \var{arg1-is-num}.\gad{NOT}())$.
- Let $\var{any-error} = \gad{OR}(\var{valid-types-and-not-div-by-zero}.\gad{NOT}(), \var{op2-not-num-or-u64-and-not-cons-or-strcons-or-hide-or-equal-or-num-equal}, \var{invalid-strcons-tag}, \\ \var{op2-is-hide-and-arg1-is-not-num}, \var{op2-is-mod-and-args-are-not-u64s}, \var{invalid-secret-tag-hide})$.
- Let $\var{op2-is-eval} = \gad{ALLOC-TAG-EQUAL}(\var{op2.tag}(), \var{globals.op2-eval-tag})$.
- Let $\var{the-cont0} = \gad{PICK}(\var{any-error}, \var{globals.error-ptr-cont}, \var{continuation})$.
- Let $\var{the-cont} = \gad{PICK}(\var{op2-is-eval}, \var{continuation}, \var{the-cont0})$.
- Let $\var{the-expr0} = \gad{pick}(\var{any-error}, \var{result}, \var{arithmetic-result})$.
- Let $\var{the-expr} = \gad{PICK}(\var{op2-is-eval}, \var{arg1}, \var{the-expr0})$.
- Let $\var{the-env} = \gad{PICK}(\var{op2-is-eval}, \var{arg2}, \var{env})$.
- Let $\var{make-thunk-num} = \gad{BOOLEAN-TO-NUM}(\var{op2-is-eval}.\gad{NOT}())$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{cont-tag.binop2}, \var{the-expr}, \var{the-env}, \var{the-cont}, \var{make-thunk-num}, \var{globals.false-num})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~if}}$.
- Let $\var{unevaled-args} = \var{cont-components}[0]$.
- Let $\var{continuation} = \var{cont-components}[1]$.
- Let $\var{condition} = \var{result}$.
- Let $\var{cont-is-if} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.if-cont-tag})$.
- Let $\var{if-not-dummy} = \gad{AND}(\var{cont-is-if}, \var{not-dummy})$.
- Let $(\var{arg1}, \var{more}) = \gad{CAR-CDR-NAMED}(\var{unevaled-args}, \var{cons-names.unevaled-args}, \var{allocated-cons-witness}, \var{if-not-dummy})$.
- Let $\var{condition-is-nil} = \var{condition}.\gad{IS-NIL}()$.
- Let $(\var{arg2}, \var{end}) = \gad{CAR-CDR-NAMED}(\var{more}, \var{cons-names.unevaled-args-cdr}, \var{allocated-cons-witness}, \var{if-not-dummy})$.
- Let $\var{end-is-nil} = \var{end}.\gad{IS-NIL}()$.
- Let $\var{res} = \gad{PICK}(\var{condition-is-nil}, \var{arg2}, \var{arg1})$.
- Let $\var{the-expr} = \gad{PICK}(\var{end-is-nil}, \var{res}, \var{arg1})$.
- Let $\var{the-cont} = \gad{PICK}(\var{end-is-nil}, \var{continuation}, \var{globals.error-ptr-cont})$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{globals.if-sym}, \var{the-expr}, \var{env}, \var{the-cont}, \var{globals.false})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~lookup}}$.
- Let $\var{saved-env} = \var{cont-components}[0]$.
- Let $\var{continuation} = \var{cont-components}[1]$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{globals.lookup-sym}, \var{result}, \var{saved-env}, \var{continuation}, \var{globals.true})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~tail}}$.
- Let $\var{saved-env} = \var{cont-components}[0]$.
- Let $\var{continuation} = \var{cont-components}[1]$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{tail}, \var{result}, \var{saved-env}, \var{continuation}, \var{globals}.\var{true})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~let}}$.
- Let $\var{var} = \var{cont-components}[0]$.
- Let $\var{body} = \var{cont-components}[1]$.
- Let $\var{let-cont} = \var{cont-components}[3]$.
- Let $\var{cont-is-let} = \gad{ALLOC-TAG-EQUAL}(\var{cont.tag}(), \var{globals.let-cont-tag})$.
- Let $\var{let-cont-is-let} = \gad{ALLOC-TAG-EQUAL}(\var{let-cont.tag}(), \var{globals.let-cont-tag})$.
- Let $\var{extended-env-not-dummy0} = \gad{AND}(\var{let-cont-is-let}, \var{not-dummy})$.
- Let $\var{extended-env-not-dummy} = \gad{AND}(\var{extended-env-not-dummy0}, \var{cont-is-let})$.
- Let $\var{extended-env} = \gad{EXTEND-NAMED}(\var{env}, \var{var}, \var{result}, \var{cons-names.env}, \var{allocated-cons-witness}, \var{extended-env-not-dummy})$.
- Let $\var{continuation-is-tail} = \gad{ALLOC-TAG-EQUAL}(\var{let-cont}.\fun{tag}(), \var{globals}.\var{tail-cont-tag})$.
- Let $\var{tail-cont} = \gad{PICK}(\var{continuation-is-tail}, \var{let-cont}, \var{newer-cont})$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{let}, \var{body}, \var{extended-env}, \var{let-cont}, \var{newer-cont2-not-dummy})$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{continuation-is-tail}.\gad{NOT}())$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~letrec}}$.
- Let $\var{var} = \var{cont-components}[0]$.
- Let $\var{body} = \var{cont-components}[1]$.
- Let $\var{letrec-cont} = \var{cont-components}[3]$.
- Let $\var{letrec-cont-is-letrec-cont} = \gad{ALLOC-TAG-EQUAL}(\var{letrec-cont.tag}(), \var{globals.letrec-cont-tag})$.
- Let $\var{extend-rec-not-dummy} = \gad{AND}(\var{letrec-cont-is-letrec-cont}, \var{not-dummy})$.
- Let $\var{extended-env} = \cir{Extend-Rec}(\var{env}, \var{var}, \var{result}, \var{allocated-cons-witness}, \var{extend-rec-not-dummy})$.
- Let $\var{is-error} = \gad{ALLOC-EQUAL}(\var{extended-env}, \var{globals}.\var{error-ptr-cont})$.
- Let $\var{continuation-is-tail} = \gad{ALLOC-TAG-EQUAL}(\var{letrec-cont}, \var{globals}.\var{tail-cont-tag})$.
- Let $\var{tail-cont} = \gad{PICK}(\var{continuation-is-tail}, \var{letrec-cont}, \var{newer-cont})$.
- Let $\var{the-cont} = \gad{PICK}(\var{is-error}, \var{globals}.\var{error-ptr-cont}, \var{tail-cont})$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{continuation-is-tail}.\gad{NOT}())$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{letrec}, \var{body}, \var{extended-env}, \var{the-cont}, \var{newer-cont2-not-dummy})$.
$\rm{\small{\bold{Case}~ cont~\bold{is}~unop}}$.
- Let $\var{unop-op1} = \var{continuation-components}[0]$.
- Let $\var{other-unop-continuation} = \var{continuation-components}[1]$.
- Let $\var{op1-is-emit} = \gad{ALLOC-TAG-EQUAL}(\var{g.op1-emit-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-eval} = \gad{ALLOC-TAG-EQUAL}(\var{g.op1-eval-tag}, \var{unop-op1.tag}())$.
- Let $\var{unop-continuation0} = \gad{PICK}(\var{op1-is-emit}, \var{newer-cont2}, \var{other-unop-continuation})$.
- Let $\var{unop-continuation} = \gad{PICK}(\var{op1-is-eval}, \var{continuation}, \var{unop-continuation0})$.
- Let $\var{result-is-cons} = \gad{ALLOC-TAG-EQUAL}(\var{g.cons-tag}, \var{result.tag}())$.
- Let $\var{result-is-str} = \gad{ALLOC-TAG-EQUAL}(\var{g.str-tag}, \var{result.tag}())$.
- Let $\var{result-is-nil} = \var{result}.\gad{IS-NIL}()$.
- Let $\var{car-cdr-is-valid} = \gad{OR}(\var{result-is-cons}, \var{result-is-str}, \var{result-is-nil})$.
- Let $\var{op1-is-car} = \gad{ALLOC-TAG-EQUAL}(\var{g.op1-car-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-cdr} = \gad{ALLOC-TAG-EQUAL}(\var{g.op1-cdr-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-car-or-cdr} = \gad{OR}(\var{op1-is-car}, \var{op1-is-cdr})$.
- Let $\var{car-cdr-is-invalid} = \gad{AND}(\var{op1-is-car-or-cdr}, \var{car-cdr-is-valid}.\gad{NOT}())$.
- Let $\var{op1-is-comm} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-comm-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-num} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-num-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-char} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-char-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-open} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-open-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-secret} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-secret-tag}, \var{unop-op1.tag}())$.
- Let $\var{op1-is-u64} = \gad{ALLOC-TAG-EQUAL}(\var{globals.op1-u64-tag}, \var{unop-op1.tag}())$.
- Let $\var{tag-is-char} = \gad{ALLOC-TAG-EQUAL}(\var{globals.char-tag}, \var{result.tag}())$.
- Let $\var{tag-is-num} = \gad{ALLOC-TAG-EQUAL}(\var{globals.num-tag}, \var{result.tag}())$.
- Let $\var{tag-is-comm} = \gad{ALLOC-TAG-EQUAL}(\var{gloabls.comm-tag}, \var{result.tag}())$.
- Let $\var{tag-is-u64} = \gad{ALLOC-TAG-EQUAL}(\var{globals.u64-tag}, \var{result.tag}())$.
- Let $\var{tag-is-num-or-comm} = \gad{OR}(\var{tag-is-num}, \var{tag-is-comm})$.
- Let $\var{tag-is-num-or-char} = \gad{OR}(\var{tag-is-num}, \var{tag-is-char})$.
- Let $\var{tag-is-num-or-comm-or-char} = \gad{OR}(\var{tag-is-num-or-comm}, \var{tag-is-char})$.
- Let $\var{tag-is-num-or-comm-or-char-or-u6}4 = \gad{OR}(\var{tag-is-num-or-comm-or-char}, \var{tag-is-u64})$.
- Let $\var{comm-invalid-tag-error} = \gad{AND}(\var{tag-is-num-or-comm}.\gad{NOT}(), \var{op1-is-comm})$.
- Let $\var{num-invalid-tag-error} = \gad{AND}(\var{tag-is-num-or-comm-or-char-or-u64}.\gad{NOT}(), \var{op1-is-num})$.
- Let $\var{char-invalid-tag-error} = \gad{AND}(\var{tag-is-num-or-char}.\gad{NOT}(), \var{op1-is-char})$.
- Let $\var{open-invalid-tag-error} = \gad{AND}(\var{tag-is-num-or-comm}.\gad{NOT}(), \var{op1-is-open})$.
- Let $\var{secret-invalid-tag-error} = \gad{AND}(\var{tag-is-num-or-comm}.\gad{NOT}(), \var{op1-is-secret})$.
- Let $\var{u64-invalid-tag-error} = \gad{AND}(\var{op1-is-u64}, \var{tag-is-num}.\gad{NOT}())$.
- Let $\var{any-error} = \gad{OR}(\var{car-cdr-is-invalid}, \var{comm-invalid-tag-error}, \var{num-invalid-tag-error}, \var{char-invalid-tag-error}, \var{open-invalid-tag-error}, \var{secret-invalid-tag-error}, \var{u64-invalid-tag-error})$.
- Let $\var{the-expr} = \gad{PICK}(\var{any-error}, \var{result}, \var{unop-val})$.
- Let $\var{the-env} = \gad{PICK}(\var{op1-is-eval}, \var{globals.nil-ptr}, \var{env})$.
- Let $\var{the-cont} = \gad{PICK}(\var{any-error}, \var{globals.error-ptr-cont}, \var{unop-continuation})$.
- Let $\var{make-thunk-num} = \gad{BOOLEAN-TO-NUM}(\var{op1-is-eval}.\gad{NOT}())$.
- Let $\var{newer-cont2-not-dummy0} = \gad{AND}(\var{op1-is-emit}, \var{any-error}.\gad{NOT}())$.
- Let $\var{newer-cont2-not-dummy} = \gad{BOOLEAN-NUM}(\var{newer-cont2-not-dummy0})$.
- Call $\var{results}.\gad{ADD-CLAUSE}(\var{cont-tag.unop}, \var{the-expr}, \var{the-env}, \var{the-cont}, \var{make-thunk-num}, \var{newer-cont2-not-dummy})$.
Make thunk #
A thunk is constructed to finish a determined layer of computation. For a certain operation, when all the input expressions are evaluated and the result is obtained in the apply-cont function, we build a thunk containing this result and an appropriate continuation pointer. We use it to terminate a Lurk program, by mapping the outermost continuation into a terminal continuation, or by propagating terminal and error continuations accordingly. Beyond that a thunk is used to return a value to the next stacked continuation, which happens for unop, binop2, lookup, tail and emit.
- $ \cir{Make-Thunk:} \\ $
- Let $\var{thunk-clauses} = \gad{MULTICASE-CLAUSES}()$.
- Let $\var{cont-is-tail} = \gad{ALLOC-EQUAL}(\var{cont.tag}(), \var{globals.tail-cont-tag})$.
- Let $\var{make-thunk-cont-not-dummy} = \gad{AND}(\var{cont-is-tail}, \var{not-dummy})$.
- Let $\var{cont-components} = \fun{get-named-components}(\var{cont}, \var{cont-names.make-thunk}, \var{allocated-cont-witness}, \var{make-thunk-cont-not-dummy})$.
- Let $\var{saved-env} = \var{cont-components}[0]$.
- Let $\var{continuation} = \var{cont-components}[1]$.
- Let $\var{result-expr} = \gad{CONSTRUCT-THUNK}(\var{result}, \var{continuation})$.
- Call $\var{thunk-clauses}.\gad{ADD-CLAUSE}(\var{tail}, \var{result-expr}, \var{env}, \var{globals}.\var{dummy-ptr})$.
- Call $\var{thunk-clauses}.\gad{ADD-CLAUSE}(\var{outermost}, \var{result}, \var{env}, \var{globals}.\var{terminal}$.
- Call $\var{thunk-clauses}.\gad{ADD-CLAUSE}(\var{terminal}, \var{result}, \var{env}, \var{globals}.\var{terminal})$.
- Call $\var{thunk-clauses}.\gad{ADD-CLAUSE}(\var{error-cont-tag}, \var{result}, \var{env}, \var{globals}.\var{error})$.
- Call $\var{thunk-clauses}.\gad{ADD-DEFAULT}(\var{thunk}, \var{env}, \var{globals}.\var{dummy-ptr})$.
- Call $\var{thunk-result} = \gad{MULTICASE}(\var{thunk-clauses})$.
- Return $(\var{thunk-result}.\var{expr}, \var{thunk-result}.\var{env}, \var{thunk-result}.\var{cont})$.
$ \cirio{INPUT} \var{result},\var{env},\var{cont},\var{not-dummy}, \var{allocated-cont-witness}$.
$ \cirio{OUTPUT} \var{expr},\var{env},\var{cont}$.
CAR-CDR-NAMED #
This gadget receives as input an allocated pointer called maybe-cons.
- $\cir{CAR-CDR-NAMED:} \\$
- Let $\var{maybe-cons-is-nil} = \var{maybe-cons}.\gad{IS-NIL}()$.
- Let $\var{cons-not-dummy} = \gad{AND}(\var{maybe-cons-is-nil}.\gad{NOT}(), \var{not-dummy})$.
- Let $(\var{allocated-car}, \var{allocated-cdr}, \var{allocated-digest}) = \var{allocated-cons-witness}.\fun{get-cons}(\var{name}, \var{cons-not-dummy}.\gad{NOT}())$.
- Let $\var{real-cons} = \gad{ALLOC-EQUAL}(\var{maybe-cons.hash}(), \var{allocated-digest})$.
- Call $\gad{IMPLIES}(\var{cons-not-dummy}, \var{real-cons})$.
- Let $\var{res-car} = \gad{PICK}(\var{maybe-cons-is-nil}, \var{globals.nil-ptr}, \var{allocated-car})$.
- Let $\var{res-cdr} = \gad{PICK}(\var{maybe-cons-is-nil}, \var{globals.nil-ptr}, \var{allocated-cdr})$.
- Return $(\var{res-car}, \var{res-cdr})$.
$ \cirio{INPUT} \var{maybe-cons}, \var{name}, \var{allocated-cons-witness}, \var{not-dummy}$.
$ \cirio{OUTPUT} \var{car},\var{cdr}$.
Extend #
We need to extend the environment for each new binding in a let expression. To extend the environment with a new binding we do the following:
- $\cir{Extend:} \\$
- Let $\var{new-binding} = \gad{CONSTRUCT-CONS-NAMED}(\var{var}, \var{val}, \var{cons-names.binding}, \var{allocated-cons-witness}, \var{not-dummy})$.
- Return $\gad{CONSTRUCT-CONS-NAMED}(\var{new-binding}, \var{env}, \var{name}, \var{allocated-cons-witness}, \var{not-dumm}y$.
$ \cirio{INPUT} \var{env}, \var{var}, \var{val}, \var{name}, \var{allocated-cons-witness}, \var{not-dummy}$.
$ \cirio{OUTPUT} \var{extended-env}$.
Extend rec #
This circuit is used to extend the recursive environment receives as input the environment env and allocated pointers to a variable var and a value val.
- $\cir{Extend-Rec:} \\$
- Let $(\var{binding-or-env}, \var{rest}) = \cir{CAR-CDR-NAMED}(\var{env}, \var{cons-names.env}, \var{allocate-cons-witness}, \var{not-dummy})$.
- Let $(\var{var-or-binding}, \var{dummy-val-or-more-bindings}) = \cir{CAR-CDR-NAMED}(\var{binding-or-env}, \var{cons-names.env-car}, \var{allocated-cons-witness}, \var{not-dummy}).$
- Let $\var{var-or-binding-is-cons} = \gad{IS-CONS}(\var{var-or-binding})$.
- Let $\var{cons} = \gad{CONSTRUCT-CONS-NAMED}(\var{var}, \var{val}, \var{cons-names.new-rec-cadr}, \var{allocated-cons-witness}, \var{not-dummy})$.
- Let $\var{list} = \gad{CONSTRUCT-CONS-NAMED}(\var{cons}, \var{globals.nil-ptr}, \var{cons-names.NewRec}, \var{allocated-cons-witness}, \var{not-dummy})$.
- Let $\var{new-env-if-sym-or-nil} = \gad{CONSTRUCT-CONS-NAMED}(\var{list}, \var{env}, \var{cons-names.extended-rec}, \var{allocated-cons-witness}, \var{not-dummy})$.
- Let $\var{cons-branch-not-dummy} = \gad{AND}(\var{var-or-binding-is-cons}, \var{not-dummy})$.
- Let $\var{cons2} = \gad{CONSTRUCT-CONS-NAMED}(\var{cons}, \var{binding-or-env}, \var{cons-names.new-rec}, \var{allocated-cons-witness}, \var{cons-branch-not-dummy})$.
- Let $\var{cons3} = \gad{CONSTRUCT-CONS-NAMED}(\var{cons2}, \var{rest}, \var{cons-names.extended-rec}, \var{allocated-cons-witness}, \var{cons-branch-not-dummy})$.
- Let $\var{is-sym} = \var{var-or-binding}.\gad{IS-SYM}()$.
- Let $\var{is-nil} = \var{var-or-binding}.\gad{IS-NIL}()$.
- Let $\var{is-sym-or-nil} = \gad{OR}(\var{is-sym}, \var{is-nil})$.
- Let $\var{is-cons} = \var{var-or-binding-is-cons}$.
- Let $\var{new-env-if-cons} = \gad{PICK}(\var{is-cons}, \var{cons3}, \var{globals.error-ptr})$.
- Let $\var{extended-env} = \gad{PICK}(\var{is-sym-or-nil}, \var{new-env-if-sym-or-nil}, \var{new-env-if-cons}$.
- Return $\var{extended-env}$.
$ \cirio{INPUT} \var{env}, \var{var}, \var{val}, \var{allocated-cons-witness}, \var{not-dummy}$.
$ \cirio{OUTPUT} \var{extended-env}$.
Low-level description #
In this section, we describe how R1CS constraints are constructed for each building block previously used in the construction of the Lurk circuit. Those components are usually called gadgets. Below is a description of how to obtain R1CS constraints for each necessary gadget.
R1CS #
We denote the witness by ${\footnotesize{w}}$, which corresponds to all the intermediate values of the subjacent program. Matrices ${\footnotesize{A,~B,~C}}$ contain the public values of the program, encoding all the constraints that the witness will have to satisfy. Specifically, it constrains the composition of gadgets that implement the reduction step. Hence, it is responsible for the validation of frame transitions.
Each frame has an Input and Output (IO), both constituted by the triple $\rm{\footnotesize{(expr,~env,~cont)}}$. The input expression is reduced frame by frame, generating a sequence of IOs where the output of a previous frame is equal to the input of the next frame. The IO is part of the witness and therefore corresponds to private data constrained in ${\footnotesize{w}}$. We say the ${\footnotesize{w}}$ satisfies ${\footnotesize{A,~B,~C}}$ if the following relation is respected:
$$\footnotesize{(A.w)~\circ~(B.w)=(C.w)}$$
where $\scriptsize{\circ}$ signifies component multiplication.
Circuit components #
In this section we describe each gadget that is necessary for the construction of the Lurk circuit in detail. We start by showing how to construct logic operations like conjunctions and disjunctions, and then we show how to implement pointers using Poseidon. Next, we present gadgets to carry out arithmetic operations, bit decomposition, and comparisons. We finally describe how to implement ternary operators, which are used to construct the case gadget, which can be used to select one among many clauses, given a key element. Multiple case gadgets can be composed into a single multicase gadget, which allows us to select multiple clauses while requiring fewer constraints than if we simply repeated the case gadget multiple times.
In order to describe R1CS constraints, we use a short notation showing the multiplications involving certain linear combinations of private variables. From this, we consider it trivial to derive the formal description presented above.
Boolean operations #
Here we show how to compute Boolean operations.
- $a.\gad{NOT}()$: given the field element $a$ that is guaranteed to be either 0 or 1, we don't need to use multiplications in order to calculate the NOT function. Instead, NOT can be computed by using the linear combination $(1 – a)$.
- $\gad{AND}(a, b)$: given two bits, $a$ and $b$, as input, we calculate the AND function using the following multiplication:
- Constrain $a \times b = \var{result}$, where $\var{result}$ corresponds to the output of the AND function.
- $\gad{OR}(a, b)$: given bits $a$ and $b$, the OR function can be calculated using both NOT and AND, using De Morgan’s law. The output is AND(a.NOT(),b.NOT()).NOT().
- $\gad{XOR}(a, b)$: given bits $a$ and $b$, the XOR function can be calculated using the formula $2.a \times b = a + b – c$, where $c$ is the result. This relation can easily be checked to be valid if and only if $c = a \oplus b$.
- $\gad{ENFORCE-IMPLICATION}(a, b)$: given bits $a$ and $b$, we say that $a$ implies $b$ if the following conditions hold:
- Call $\var{implication} = \gad{IMPLIES}(a, b)$.
- Call $\gad{ENFORCE-TRUE}(\var{implication})$.
- $\gad{ENFORCE-EQUAL}(a, b)$: given bits $a$ and $b$, we enforce equality of bits using the constraint
- Constrain $(a – b) \times 1 = 0$.
- $\gad{ENFORCE-TRUE}(a)$: given bit $a$, we call ENFORCE-EQUAL(a, 1).
- $\gad{ENFORCE-FALSE}(a)$: given bit $a$, we call ENFORCE-EQUAL(a, 0).
- $\gad{ENFORCE-BIT}(a)$: given bit $a$, we
- Constrain $(1 – a) \times a = 0$.
- $\gad{IMPLIES}(a, b)$: equivalent to $\gad{AND}(a, b.\gad{NOT}()).\gad{NOT}()$.
In Table 1 we show how many constraints and witnesses are required to construct each gadget.
| Gadget | Constraints | Witnesses |
|---|---|---|
| NOT | 0 | 0 |
| OR | 1 | 1 |
| AND | 1 | 1 |
| XOR | 1 | 1 |
| ENFORCE-IMPLICATION | 2 | 1 |
| ENFORCE-EQUAL | 1 | 0 |
| ENFORCE-TRUE | 1 | 0 |
| ENFORCE-FALSE | 1 | 0 |
| ENFORCE-BIT | 1 | 0 |
| IMPLIES | 1 | 1 |
Pointers #
In this section we describe the construction of gadgets for pointers. The basic building block is Poseidon gadget, which can be instantiated in different ways. What distinguishes each instantiation is the number of input field elements. As we increase the number of input elements, we also increase the circuit size of the gadget. Since each pointer needs two field elements to represent it, in order to create a gadget for cons operation, we to pass two allocated pointers as input, therefore we need 4 field elements and, consequently, we have to use the 4-ary instantiation of Poseidon gadget. Analogously, we need 6-ary instantiation of Poseidon gadget to construct a pointer for function, since it needs to pass as input 3 allocated pointers, namely the argument, the body and the environment. Finally, we may need to pass 4 allocated pointers to create generic pointers, as for example is required for some continuation pointers.
Next we describe different gadgets that we provide to construct different types of pointers.
- $\gad{ALLOC-NUM}(n)$: given a field element n as input, it allocates a new variable whose value is n. There is no constraint for this gadget. It is only necessary to allocate a new witness in the circuit.
- $\gad{ALLOC-PTR}(\var{tag}, \var{hash})$: given a pair of field elements, tag and hash as input, it proceed as follows:
- $\gad{ALLOC-NUM}(\var{tag})$.
- $\gad{ALLOC-NUM}(\var{hash})$.
- $\gad{ALLOC-CONSTANT}(c)$: given a field element $c$ as input, it allocates a new pointer whose value is $c$. Namely, the constraint is implemented as:
- Constrain $\rm{allocated-output} \times 1 = c$.
- $\gad{ALLOC-CONSTANT-PTR}(c)$: given a pointer $c$ to a constant value, it allocates the pointer in the circuit as follows:
- Let $\var{alloc-tag} = \gad{ALLOC-CONSTANT}(c.\fun{tag}())$.
- Let $\var{alloc-hash} = \gad{ALLOC-CONSTANT}(c.\fun{hash}())$.
- $\gad{ALLOC-CONSTANT-CONT-PTR}(c)$: given a continuation pointer $c$ to a constant value, it allocates the pointer in the circuit as follows:
- Let $\var{alloc-tag} = \gad{ALLOC-CONSTANT}(c.\fun{tag}())$.
- Let $\var{alloc-hash} = \gad{ALLOC-CONSTANT}(c.\fun{hash}())$.
- $\gad{ALLOC-FROM-PARTS}(\var{tag}, \var{hash})$: it receives as input two field elements, as allocated numbers, that can be used to allocate a new pointer in the circuit. No constraints are required for this purpose.
- $\gad{ALLOC-EQUAL}(a, b)$: it receives as input two allocated numbers, $a$ and $b$, and as output it gives us a Boolean that indicates if $a$ is equal to $b$ or not.
- Let $\var{diff} = \gad{SUB}(a – b)$.
- Let $\var{result} = \gad{ALLOC-BIT}(a == b)$.
- Constrain $\var{result} \times \var{diff} = 0$.
- Constrain $(\var{diff} + \var{result}) \times q = 1$.
- $\gad{ALLOC-TAG-EQUAL}(a, b)$: it receives as input two numbers, where $a$ is an allocated number and $b$ is a constant, and as output it gives us a Boolean that indicates if $a$ is equal to $b$ or not. It works in the same way as $\gad{ALLOC-EQUAL}, but avoids the unnecessary allocation of tag constants as global variables.
- Let $\var{diff} = \gad{SUB}(a – b)$.
- Let $\var{result} = \gad{ALLOC-BIT}(a == b)$.
- Constrain $\var{result} \times \var{diff} = 0$.
- Constrain $(\var{diff} + \var{result}) \times q = 1$.
- $\gad{IS-SYM(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `symbol` tag.
- $\gad{IS-FUN(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `function` tag.
- $\gad{IS-CONS(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `cons` tag.
- $\gad{IS-STR(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `string` tag.
- $\gad{IS-NUM(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `number` tag.
- $\gad{IS-U64(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `u64` tag.
- $\gad{IS-CHAR(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `char` tag.
- $\gad{IS-COMM(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `comm` tag.
- $\gad{IS-THUNK(a)}$: the same as $\gad{ALLOC-TAG-EQUAL}(a, c)$, where $c$ represents the field element whose value corresponds to the `thunk` tag.
- $\gad{ALLOC-IS-ZERO}(a)$: it receives as input an allocated number $a$. The output is given by a Boolean that indicates if the input number is zero or not. It is constructed as follows:
- Let $\var{is-zero} = (a == 0)$.
- Let $\var{result} = \gad{ALLOC-BIT}(\var{is-zero})$.
- Constrain $\var{result} \times a = 0$.
- Constrain $(x + \var{result}) \times q = 1$.
- $\gad{ALLOCATE-DUMMY-COMPONENTS}()$: it receives no input argument and is responsible for allocating dummy variables and creating a pointer for them. Concretely, we have the following:
- Let $\var{value} = \gad{ALLOC-FROM-PARTS}(0, 0)$.
- Let $\var{cont} = \gad{ALLOC-FROM-PARTS}(0, 0)$.
- Let $\var{dummy-hash} = \gad{CONSTRUCT-THUNK}(\var{value}, \var{cont})$.
- $\gad{ALLOCATE-THUNK-COMPONENTS}()$: it allocate thunk components
- $\gad{ALLOCATE-HASH-COMPONENTS}$
- $\gad{CONSTRUCT}(\var{components})$: it receives as input 4 allocated pointers, represented as 8 field elements, and calls the 8-ary Poseidon gadget.
- $\gad{CONSTRUCT-CONS}(\var{components})$: it receives as input 2 allocated pointers, represented as 4 field elements, and calls the 4-ary Poseidon gadget.
- $\gad{CONSTRUCT-THUNK}(\var{components})$: it receives as input 2 allocated pointers, represented as 4 field elements, and calls the 4-ary Poseidon gadget.
- $\gad{CONSTRUCT-FUN}(\var{components})$: it receives as input 3 allocated pointers, represented as 6 field elements, and calls the 6-ary Poseidon gadget.
- $\gad{CONSTRUCT-LIST}(\var{elements})$: it receives as input a list of n allocated pointers and uses `cons` $n – 1$ times in order to construct a pointer to the output list.
| Gadget | Constraints | Witnesses |
|---|---|---|
| ALLOC-NUM | 0 | 1 |
| ALLOC-PTR | 0 | 2 |
| ALLOC-CONSTANT | 1 | 1 |
| ALLOC-CONSTANT-CONT-PTR | 2 | 2 |
| ALLOC-FROM-PARTS | 0 | 0 |
| ALLOC-EQUAL | 4 | 3 |
| ALLOC-TAG-EQUAL | 3 | 2 |
| IS-SYM | 3 | 2 |
| IS-FUN | 3 | 2 |
| IS-CONS | 3 | 2 |
| IS-STR | 3 | 2 |
| IS-NUM | 3 | 2 |
| IS-U64 | 3 | 2 |
| IS-CHAR | 3 | 2 |
| IS-COMM | 3 | 2 |
| IS-THUNK | 3 | 2 |
| ALLOC-IS-ZERO | 3 | 2 |
| ALLOCATE-THUNK-COMPONENTS | 289 | 293 |
| ALLOCATE-MAYBE-DUMMY-COMPONENTS | 390 | 398 |
| ALLOCATE-MAYBE-FUN | 339 | 345 |
| CONSTRUCT | 388 | 388 |
| CONSTRUCT-CONS | 286 | 284 |
| CONSTRUCT-THUNK | 286 | 284 |
| CONSTRUCT-FUN | 334 | 334 |
| CONSTRUCT-COMMITMENT | 334 | 334 |
| CONSTRUCT-LIST | 286(n – 1) | 284(n – 1) |
Functional Commitments #
- $\gad{SECRET}(\var{commitment})$:
- Check if the opening is known. If so, name it $(\var{secret}, \var{payload})$.
- Let $\var{open-commitment} = \gad{CONSTRUCT-COMMITMENT}(\var{secret}, \var{payload})$.
- Let $\var{valid-opening} = \gad{ALLOC-EQUAL}(\var{commitment}, \var{open-commitment})$.
- Return $\var{secret}$.
- $\gad{NUM}(\var{value})$:
- Let $\var{num-value} = \var{value.hash}()$.
- Let $\var{alloc-num-res} = \gad{ALLOC-FROM-PARTS}(\var{globals.num-tag}, \var{num-value})$.
- Return $\var{alloc-num-res}$.
- $\gad{CHAR}(\var{value})$:
- Let $\var{char-value} = \var{value.hash}()$.
- Let $\var{alloc-char-res} = \gad{ALLOC-FROM-PARTS}(\var{globals.char-tag}, \var{char-value})$.
- Return $\var{alloc-char-res}$.
- $\gad{COMM}(\var{value})$:
- Let $\var{comm-value} = \var{value.hash}()$.
- Let $\var{alloc-comm-res} = \gad{ALLOC-FROM-PARTS}(\var{globals.comm-tag}, \var{comm-value})$.
- Return $\var{alloc-comm-res}$.
| Gadget | Constraints | Witnesses |
|---|---|---|
| HIDE | 334 | 334 |
| COMMIT | 334 | 334 |
| OPEN | 334 | 334 |
| SECRET | 334 | 334 |
| NUM | 0 | 0 |
| CHAR | 0 | 0 |
| COMM | 0 | 0 |
Arithmetic operations #
Here we present all the arithmetic operations that are required to implement the Lurk circuit. For each operation, we provide two gadgets. The first receives both input and output terms, constraining them so that it really corresponds to the correct calculation of that operation. The second only receives the input terms, and it is the responsibility of the gadget to allocate the output and calculate it accordingly.
- $\gad{SUM}(a, b, \var{res})$: It receives as input the two operands and the result as allocated numbers.
- Constrain: $(a + b) \times (1) = \var{res}$.
- $\gad{ADD}(a, b)$: In this case, no result is provided. We first need to allocate and assign the correct value.
- Let $\var{res} = \gad{ALLOC}(a + b)$.
- Call $\gad{SUM}(a, b, \var{res})$.
- $\gad{DIFFERENCE}(a, b, \var{res})$: It receives as input the two operands and the result as allocated numbers.
- Constrain: $(\var{res} + b) \times (1) = a$.
- SUB(a, b): In this case no result is provided. We first need to allocate and assign the correct value.
- Let $\var{res} = \gad{ALLOC}(a – b)$.
- Call $\gad{DIFFERENCE}(a, b, \var{res})$.
- $\gad{PRODUCT}(a, b, \var{res})$: It receives as input the two operands and the result as allocated numbers.
- Constrain: $(a) \times (b) = \var{res}$.
- $\gad{MUL}(a, b)$: In this case no result is provided. We first need to allocate and assign the correct value.
- Let $\var{res} = \gad{ALLOC}(a.b)$.
- Call $\gad{PRODUCT}(a, b, \var{res})$.
- $\gad{DIV}(a, b)$: For division, we multiply by the inverse.
- Let $\var{inv} = \gad{ALLOC}(b^{-1})$
- Let $\var{res} = \gad{MUL}(a, \var{inv})$.
| Gadget | Constraints | Witnesses |
|---|---|---|
| SUM | 1 | 0 |
| ADD | 1 | 1 |
| DIFFERENCE | 1 | 0 |
| SUB | 1 | 1 |
| PRODUCT | 1 | 0 |
| MUL | 1 | 1 |
| DIV | 1 | 1 |
Comparisons #
We have that a number is defined to be negative if the parity bit (the least significant bit) is odd after doubling, meaning that the field element (after doubling) is larger than the underlying prime p that defines the field, then a modular reduction must have been carried out, changing the parity that should be even (since we multiplied by 2) to odd. In other words, we define negative numbers to be those field elements that are larger than $p/2$.
Operations like ﹤, ≤, ﹥, ≥ are implemented using the bit decomposition 3 times. To test if $a < b$, we calculate the difference $\var{diff} = (b – a)$ and test if diff is negative by seeing if the parity bit, the least significant bit, of $2\var{diff}$ is 1. If it is the case, it means $2\var{diff}$ is larger than $p$. Therefore, after computing the modular reduction, the parity bit is changed from 0 to 1. By composing with equality tests and other basic Boolean operations, we also obtain ≤, ﹥, ≥.
- $ \gad{IS-NEGATIVE:} \\ $
- Let $\var{double-num} = \gad{ADD}(\var{num}, \var{num})$.
- Let $\var{double-num-bits} = \var{double-num}.\cir{to-bits-le-strict}()$.
- Let $\var{lsb-2num} = \var{double-num-bits}[0]$.
- Let $\var{num-is-negative} = \var{lsb-2num}$.
- Return $\var{num-is-negative}$.
$ \cirio{INPUT} \var{num}$.
$ \cirio{OUTPUT} \var{num-is-negative}$.
In order to compare 2 field elements, we first compute the predicate $\cir{Is-Negative}()$ for $a$, $b$ and $(b - a)$, which are input parameters. Then we use a multicase to select the desired result according to the operation given by $\var{op2}$.
- $ \gad{COMPARISON-HELPER:} \\ $
- Let $\var{a-is-negative} = \gad{Is-Negative}(a)$.
- Let $\var{b-is-negative} = \gad{Is-Negative}(b)$.
- Let $\var{diff-is-negative} = \gad{Is-Negative}(\var{diff})$.
- Let $\var{diff-is-zero} = \gad{ALLOC-IS-ZERO}(\var{diff})$.
- Let $\var{diff-is-not-positive} = \gad{OR}(\var{diff-is-positive}, \var{diff-is-zero})$.
- Let $\var{diff-is-positive} = \gad{AND}(\var{diff-is-negative}.\gad{NOT}(), \var{diff-is-zero}.\gad{NOT}())$.
- Let $\var{diff-is-not-negative} = \var{diff-is-negative}.\gad{NOT}()$.
- Let $\var{not-one-negative-and-other-not-negative} = \gad{XOR}(\var{a-is-negative}, \var{b-is-negative})$.
- Let $\var{a-negative-and-b-not-negative} = \gad{AND}(\var{a-is-negative}, \var{b-is-negative}.\gad{NOT}())$.
- Let $\var{alloc-num-diff-is-negative} = \gad{BOOLEAN-TO-NUM}(\var{diff-is-negative})$.
- Let $\var{alloc-num-diff-is-not-positive} = \gad{BOOLEAN-TO-NUM}(\var{diff-is-not-positive})$.
- Let $\var{alloc-num-diff-is-positive} = \gad{BOOLEAN-TO-NUM}(\var{diff-is-positive})$.
- Let $\var{alloc-num-diff-is-not-negative} = \gad{BOOLEAN-TO-NUM}(\var{diff-is-not-negative})$.
- Let $\var{comp-clauses} = \gad{CASE-CLAUSES}()$.
- Let $\var{comp-clauses}.\gad{ADD-CLAUSE}(\var{alloc-num-diff-is-negative}, \var{globals.true}, \var{globals.false})$.
- Let $\var{comp-clauses}.\gad{ADD-CLAUSE}(\var{alloc-num-diff-is-not-positive}, \var{globals.true}, \var{globals.false})$.
- Let $\var{comp-clauses}.\gad{ADD-CLAUSE}(\var{alloc-num-diff-is-positive}, \var{globals.false}, \var{globals.true})$.
- Let $\var{comp-clauses}.\gad{ADD-CLAUSE}(\var{alloc-num-diff-is-not-negative}, \var{globals.false}, \var{globals.true})$.
- Let $\var{comp-result} = \gad{MULTICASE}(\var{op2.tag}(), \var{comp-clauses}, \var{comp-default})$.
- Let $\var{comp-val-same-sign-num} = \var{comp-result}[0]$.
- Let $\var{comp-val-a-neg-and-b-not-neg-num} = \var{comp-result[1]}$.
- Let $\var{comp-val-a-not-neg-and-b-neg-num} = \var{comp-result[2]}$.
- Let $\var{is-comparison-tag} = \var{comp-result.is-default}.\gad{NOT}()$.
- Let $\var{comp-val1} = \gad{PICK}(\var{a-negative-and-b-not-negative}, \var{comp-val-a-neg-and-b-not-neg-num}, \var{comp-val-a-not-neg-and-b-neg-num})$.
- Let $\var{comp-val2} = \gad{PICK}(\var{not-one-negative-and-b-not-negative}, \var{comp-val-same-sign-num}, \var{comp-val1})$.
- Let $\var{comp-val-is-zero} = \gad{ALLOC-IS-ZERO}(\var{comp-val2})$.
- Let $\var{comp-val} = \gad{PICK}(\var{comp-val-is-zero}, \var{globals.nil-ptr}, \var{globals.t-ptr})$.
- Return $(\var{is-comparison-tag}, \var{comp-val}, \var{diff-is-negative})$.
$ \cirio{INPUT} a, b, \var{diff}, \var{op2}$.
$ \cirio{OUTPUT} \var{is-comparison-tag}, \var{comp-val}, \var{diff-is-negative}$.
Next we define an auxiliary function that is responsible for constraining the coercion from field element to an unsigned integer. To do that, we use big number to calculate the remainder after division by an appropriate power of 2, depending on the $\var{size}$. Later, we use the $\gad{LINEAR}()$ gadget to constrain the relation $a = b.q + r$, where $q$ is the power of 2 mentioned above, and $0 \leq r < q$.
- $ \gad{TO-UNSIGNED-INTEGER-HELPER:} \\ $
- Let $\var{power-of-two-bn} = \fun{pow}(2, \var{size})~-$ computed as a big number.
- Let $(\var{q-bn}, \var{r-bn}) = \var{field-bn.div-rem}(\var{power-of-two-bn})$.
- Let $\var{q-num} = \gad{ALLOCATE-UNCONSTRAINED-BIGNUM}(\var{q-bn})$.
- Let $\var{r-num} = \gad{ALLOCATE-UNCONSTRAINED-BIGNUM}(\var{r-bn})$.
- Let $\var{pow2-size} = \fun{field-pow}(2, \var{size})~-$ computed as a field element.
- Call $\gad{LINEAR}(\var{q-num}, \var{pow2-size}, \var{r-num}, \var{field-elem})$.
- Let $\var{r-bits} = \var{field-elem-bits}[0 \var{..size}]$.
- Call $\gad{ENFORCE-PACK}(\var{r-bits}, \var{r-num})$.
$ \cirio{INPUT} \var{field-elem}, \var{field-bn}, \var{field-elem-bits}, \var{size}$.
$ \cirio{OUTPUT} \var{r-num}$.
Next we present an auxiliary function that converts from num to unsigned integers by taking the least significant bits. The output is a pair of allocated numbers, where the first one corresponds to the u32 coercion, while the second corresponds to the u64 coercion.
- $ \gad{TO-UNSIGNED-INTEGERS:} \\ $
- Let $\var{field-bn} = \fun{from-bytes-le}(\var{num})$.
- Let $\var{field-elem-bits} = \var{num.to-bits-le}()$.
- Let $\var{r32-num} = \gad{TO-UNSIGNED-INTEGER-HELPER}(\var{maybe-unsigned}, \var{field-bn}, \var{field-elem-bits}, 32)$.
- Let $\var{r64-num} = \gad{TO-UNSIGNED-INTEGER-HELPER}(\var{maybe-unsigned}, \var{field-bn}, \var{field-elem-bits}, 64)$.
- Return $(\var{r32-num}, \var{r64-num})$.
$ \cirio{INPUT} \var{num}$.
$ \cirio{OUTPUT} \var{r32-num}, \var{r64-num}$.
| Gadget | Constraints | Witnesses |
|---|---|---|
| IS-NEGATIVE | 389 | 388 |
| COMPARISON-HELPER | 1215 | 1208 |
| TO-UNSIGNED-INTEGER-HELPER | 2 | 2 |
| TO-UNSIGNED-INTEGERS | 360 | 259 |
Coercion #
- $ \gad{TO-U64:} \\ $
- Let $\var{field-bn} = \fun{from-bytes-le}(\var{maybe-u64.to-bytes-le})$.
- Let $\var{field-elem-bits} = \var{maybe-u64.to-bits-le}()$.
- Let $\var{r64-num} = \gad{TO-UNSIGNED-INTEGER-HELPER}(\var{maybe-unsigned}, \var{field-bn}, \var{field-elem-bits}, 64)?$.
- Return $(\var{r64-num})$.
$ \cirio{INPUT} \var{maybe-u64}$.
$ \cirio{OUTPUT} \var{r64-num}$.
Next we enforce div and mod operation for U64. We need to show that $\var{arg1} = q.\var{arg2} + r$, such that $0 \leq r < \var{arg2}$.
- $ \gad{ENFORCE-U64-DIV-MOD:} \\ $
- Let $\var{arg1-u64} = \var{arg1.to-u64-unchecked}()$.
- Let $\var{arg2-u64} = \var{arg2.to-u64-unchecked}()$.
- Let $(q, r) = \fun{If}~ \var{arg2-u64} \neq 0 ~\fun{Return}~ {(\var{arg1-u64} / \var{arg2-u64}, \var{arg1-u64} \pmod{\var{arg2-u64}})} ~\fun{Else Return}~ {(0, 0)}~-$ If denominator is zero, replace by dummies.
- Let $\var{alloc-r-num} = \gad{ALLOC}(r)$.
- Let $\var{alloc-q-num} = \gad{ALLOC}(q)$.
- Let $\var{alloc-arg1-num} = \gad{ALLOC}(\var{arg1-u64})$.
- Let $\var{alloc-arg2-num} = \gad{ALLOC}(\var{arg2-u64})$.
- Let $\var{product-u64mod} = \gad{MUL}(\var{alloc-q-num}, \var{alloc-arg2-num})$.
- Let $\var{sum-u64mod} = \gad{ADD}(\var{product-u64mod}, \var{alloc-r-num})$.
- Let $\var{u64mod-decomp} = \gad{ALLOC-EQUAL}(\var{sum-u64mod}, \var{alloc-arg1-num})$.
- Let $\var{b-is-zero} = \gad{alloc-is-zero}(\var{arg2.hash}())$.
- Let $\var{b-is-not-zero-and-cond} = \gad{AND}(\var{b-is-zero}.\gad{NOT}(), \var{cond})$.
- Call $\gad{ENFORCE-IMPLICATION}(\var{b-is-not-zero-and-cond}, \var{u64mod-decomp})$.
- Call $\gad{enforce-less-than-bound}(\var{cond}, \var{alloc-r-num}, \var{alloc-arg2-num})$.
- Return $(\var{alloc-q-num}, \var{alloc-r-num})$.
$ \cirio{INPUT} \var{cond}, \var{arg1}, \var{arg2}$.
$ \cirio{OUTPUT} (\var{alloc-q-num}, \var{alloc-r-num})$.
Given that $\var{cond}$ is satisfied, next we enforce the $\var{num} < \var{bound}$. This is done by proving $(\var{bound} - \var{num})$ is positive. $\var{num}$ and $\var{bound}$ must be a positive field element. $\var{cond}$ is a Boolean condition that enforces the validation if and only if it is true.
- $ \gad{ENFORCE-LESS-THAN-BOUND:} \\ $
- Let $\var{diff-bound-num} = \gad{SUB}(\var{bound}, \var{num})$.
- Let $\var{diff-bound-num-is-negative} = \gad{ALLOCATE-IS-NEGATIVE}(\var{diff-bound-num})$.
- Call $\gad{ENFORCE-IMPLICATION}(\var{cond}, \var{diff-bound-num-is-negative}.\gad{NOT}())$.
$ \cirio{INPUT} \var{cond}, \var{num}, \var{bound}$.
Next we convert from bn to num. This allocation is NOT constrained here. In the circuit we use it to prove u64 decomposition, since using bn we have division with remainder, which is used to find the quotient after dividing by 2ˆ64. Therefore we constrain this relation afterwards. In order to do that we use an external library for big number arithmetic, because in finite field we can´t compute the Euclidean division.
- $ \cir{ALLOCATE-UNCONSTRAINED-BIGNUM:} \\ $
- Let $\var{bytes-le} = \var{bn.to-bytes-le}()$.
- Pad $\var{bytes-le}$ with zeros, such that it has length 32.
- Let $\var{num} = \gad{ALLOC}(\var{bytes-le})$.
- Return $\var{num}$.
$ \cirio{INPUT} \var{bn}$.
$ \cirio{OUTPUT} \var{num}$.
| Gadget | Constraints | Witnesses |
|---|---|---|
| $\gad{TO-U64}$ | 258 | 257 |
| $\gad{ENFORCE-U64-DIV-MOD}$ | 404 | 403 |
| $\gad{ENFORCE-LESS-THAN-BOUND}$ | 392 | 390 |
| $\gad{ALLOCATE-UNCONSTRAINED-BIGNUM}$ | 0 | 1 |
Bit decomposition #
We use a gadget from the bellperson [^Bellperson] library, called $\fun{to-bits-le-strict}(a)$, in order to decompose field elements into bit representation.
$\fun{to-bits-le-strict}(a)$ returns a vector of Booleans corresponding to the bits of $a$ using little endian representation.
| Gadget | Constraints | Witnesses |
|---|---|---|
| $\gad{BIT-DECOMP-LE}$ | 388 | 387 |
Equality #
All operations described in this section are binary operations, a detailed description of which can be found in Apply continuation Section. Here, we explain how each operation is implemented. There is not a gadget construction for each of them, however. Their implementation is part of the binop and binop2 in $\cir{Apply-Continuation}$.
- Number equality. This is easily implemented using $\gad{ALLOC-EQUAL}$.
- Equality of expressions (recursive). This is obtained by testing equality of hashes.
Conditionals #
We use ternary operators to construct conditionals. The main building block is the gadget that can select a field element, given a boolean condition.
- $\gad{PICK-FIELD-ELEMENT}(\var{condition}, a, b)$ If $\var{condition}$ is $\var{true}$, ensure $\var{res} = a$. Otherwise, ensure $\var{res} = b$.
- Let $\var{res}$ be
- If $\var{condition}$, then let $\var{res} = \gad{ALLOC}(a)$.
- Otherwise, let $\var{res} = \gad{ALLOC}(b)$.
- Constrain: $(b – a) \times \var{condition}=(b – \var{res})$.
- Let $\var{res}$ be
In order to pick a pointer we define the next gadget.
- $\gad{PICK}(\var{condition}, a, b):$
- Let $\var{res-tag} = \gad{PICK-FIELD-ELEMENT}(\var{condition}, \var{a.tag}(), \var{b.tag}())$.
- Let $\var{res-hash} = \gad{PICK-FIELD-ELEMENT}(\var{condition}, \var{a.hash}(), \var{b.hash}())$.
- Return $\var{res} = \gad{ALLOC-FROM-PARTS}(\var{res-tag}, \var{res-hash})$.
| Gadget | Constraints | Witnesses |
|---|---|---|
| $\gad{PICK-FIELD-ELEMENT}$ | 1 | 1 |
| $\gad{PICK}$ | 2 | 2 |
Multicase #
The multicase gadget is particularly important for Lurk, since it is a core part of $\cir{Reduce-Cons}()$ and $\cir{Apply-Continuation}()$, which are essential components in reduction of expressions. In summary, a multicase is a combination of multiple case gadgets, eliminating common constraints.
A clause is given by a pair of field elements denoted by $(\var{key}, \var{value})$. A case statement is given by a set of clauses where no repeated keys appear. Also, it has a default clause, which is used when no key satisfies the one given as input.
A multicase is a set of cases where the same sequence of keys is used for each case, including their order. This way, we can calculate a $\var{selector}$ which will be applied for every case. We constrain the selector only once, avoiding unnecessary circuit growth. The strategy to enforce selection is the following:
- Selector: allocate one bit per clause.
- Test that if after adding all selectors we get 1, then exactly one is true, since each element is a bit.
- Enforce selected key.
For the first case clauses, we calculate all the constraints a case gadget has, as follows:
- Constrain: $$ \var{acc} = \prod_i{(key_i- \var{selected})} $$
such that $\var{acc}$ is zero if and only if some key is selected.
- $\var{is-selected}= \gad{ALLOC-IS-ZERO}(\var{acc})$.
Now, for the next cases, some constraints do not need to be repeated. We can proceed by computing the constraints of the result, by calculating the dot product of the selector and the values.
- Let $\var{sum}$ be initialized with zero.
- For each clause $c$:
- $\var{sum} = \var{sum} + \gad{PICK}(\var{selector}, c.\var{value}, 0)$.
Finally, we need to constrain the default result, which follows:
- Let $\var{res}$ be:
- If $\var{is-selected}$ is true, return $\var{sum}$.
- Otherwise, return $\var{default}$.
The number of constraints for a case gadget is given by $7 + 4c$, where $c$ corresponds to the number of clauses in it. Moreover, the number of witnesses is given by $11 + 4c$.
For the multicase, we have that the number of constraint is $\var{cost-of-case} + 4(m – 1)$, where $m$ is the number of cases. Furthermore, the number of witnesses is $\var{cost-of-case} + 5(m – 1)$.
Final Remarks #
In this document, we presented Lurk’s circuit specification, demonstrating how Lurk programs are proved in zero-knowledge. The total size of the circuit (as of January 2023) is 12513 constraints and 12140 witnesses. Being able to reduce generic Lurk expressions to such a small frame size allows us to use recursive SNARKs efficiently. In particular, we plan to integrate Nova folding techniques to obtain further performance improvements.
The reader wanting more information about Lurk will find several references below, including the Lurk evaluation specification 22 and the Lurk reduction notes [ˆLurk-reduction-note].
References #
Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof-systems._ In STOC 1985, pages 291–304, 1985 ↩︎
Benarroch, D., Gurkan, K., Kahat, R., Nicolas, A., & Tromer, E. (2019). zkInterface, a standard tool for zero-knowledge interoperability._ [^Bellperson] Bellperson implementation. github, 2021. https://github.com/filecoin-project/bellperson ↩︎
Rosario Gennaro, Craig Gentry, Bryan Parno, and Mariana Raykova. Quadratic span programs and succinct NIZKs without PCPs._ ↩︎
Bryan Parno, Jon Howell, Craig Gentry, and Mariana Raykova. Pinocchio: Nearly practical verifiable computation ↩︎
Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, and Madars Virza. SNARKs for C: Verifying program executions succinctly and in zero knowledge, Cryptology ePrint Archive, Report 2013/507, 2013. ↩︎
Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, and Madars Virza. Succinct non-interactive zero knowledge for a von Neumann architecture._ In USENIX Security 2014, pages 781–796, 2014. ↩︎
Jens Groth. On the size of pairing-based non-interactive arguments._ In proc. Eurocrypt ’16, Part II, pages 305–326, 2016. ↩︎
Yuri Gurevich, Evolving Algebras, IFIP 1994. ↩︎
Kothapalli, A., Setty, S., Tzialla, I. (2022 ) Nova: Recursive Zero-Knowledge Arguments from Folding Schemes, Cryptology ePrint Archive, Report 2021/370, 2021. https://ia.cr/2021/370. ↩︎
Gailly, N., Maller, M., Nitulescu, A., SnarkPack: Practical SNARK Aggregation, Cryptology ePrint Archive, Paper 2021/529. ↩︎
A good source of information on CPS is the book “Essentials of Programming Languages” 13 ↩︎
Sean Bowe, Jack Grigg, and Daira Hopwood. Recursive proof composition without a trusted setup. Cryptology ePrint Archive, Report 2019/1021, 2019. https://ia.cr/2019/1021. ↩︎
Daniel P. Friedman and Mitchell Wand. Essentials of Programming Languages, 3rd Edition. The MIT Press, 3 edition, 2008. ↩︎
Lorenzo Grassi, Dmitry Khovratovich, Christian Rechberger, Arnab Roy, and Markus Schofnegger. Poseidon: A new hash function for zero-knowledge proof systems. Cryptology ePrint Archive, Report 2019/458, 2019. https://ia.cr/2019/458. ↩︎
Hopwood, Daira, et al. “Zcash protocol specification.” version 2022.3.8, 2016 §5.4.9.6 ↩︎
Virza, Madars, On deploying succinct zero-knowledge proofs, https://dspace.mit.edu/handle/1721.1/113986 ↩︎
Neptune: reference Poseidon implementation. github, 2021. https://github.com/filecoin-project/neptune/ ↩︎
Benoît Libert, Somindu C. Ramanna, and Moti Yung. Functional commitment schemes: From polynomial commitments to pairing-based accumulators from simple assumptions. Cryptology ePrint Archive, Paper 2016/766, 2016. https://eprint.iacr.org/2016/766. ↩︎
Helger Lipmaa and Kateryna Pavlyk. Succinct functional commitment for a large class of arithmetic circuits. Cryptology ePrint Archive, Paper 2021/932, 2021. https://eprint. iacr.org/2021/932. ↩︎
Chris Peikert, Zachary Pepin, and Chad Sharp. Vector and functional commitments from lattices. Cryptology ePrint Archive, Paper 2021/1254, 2021. https://eprint.iacr.org/ 2021/1254. ↩︎
Dan Boneh, Wilson Nguyen, and Alex Ozdemir. Efficient functional commitments: How to commit to a private function. Cryptology ePrint Archive, Paper 2021/1342, 2021. https://eprint.iacr.org/2021/1342 ↩︎
Lurk evaluation notes. github, 2022. https://github.com/lurk-lab/lurk-rs/blob/master/notes/eval.md ↩︎
